A port of the MATLAB Delta Sigma Toolbox based on free software and very little sleep.
| Author: | Giuseppe Venturini, based on Richard Schreier’s work, who deserves most of the credit. |
|---|---|
| Release: | 0.2.2 |
| Date: | August 05, 2016 |
Homepage: http://www.python-deltasigma.io
Documentation: http://docs.python-deltasigma.io
Repository: https://github.com/ggventurini/python-deltasigma
Bug tracker: https://github.com/ggventurini/python-deltasigma/issues
Introduction¶
Python-deltasigma is a Python package to synthesize, simulate, scale and map to implementable structures delta sigma modulators.
It aims to provide a 1:1 Python port of Richard Schreier’s *excellent* MATLAB Delta Sigma Toolbox, the de facto standard tool for high-level delta sigma simulation, upon which it is very heavily based.
Contents¶
Status¶
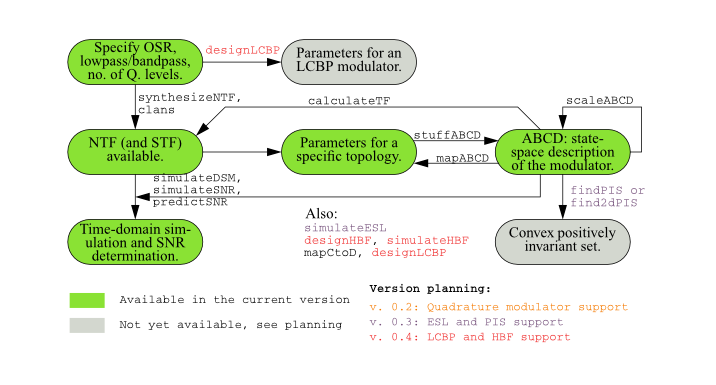
This project is a work in progress, not all functionality has been ported, yet. The next figure shows the relationship between the main functions and the available functionality at a glance.
A detailed change log may be found in CHANGES.rst.
Detailed information split by file and function status may be found in files.csv.
The further functionality is expected to be ported and available in future releases according to the ROADMAP.
Examples¶
To see the currently implemented functionality in action, take a look at the following ipython notebooks:
- dsdemo1,
notebook port of the interactive
dsdemo1.m. - dsdemo2,
notebook port of the interactive
dsdemo2.m. - dsdemo3,
notebook port of the interactive
dsdemo3.m. - dsdemo4,
notebook port of
dsdemo4.m. Audio file, right click to download. - MASH example, an example of the simulation of a MASH cascade.
- dsexample1, Python
version of
dsexample1.m. - dsexample2, Python
version of
dsexample2.m. - dsexample3, Python
version of
dsexample3.m. - dsexample4, Python
version of
dsexample4.m.
They are also a good means for getting started quickly.
If you have some examples you would like to share, send me a mail, and I will add them to the above list.
Install¶
Supported platforms¶
python-deltasigma runs on every platform and arch. supported by its dependencies:
- Platforms: Linux, Mac OS X, Windows.
- Archs: x86, x86_64 and armf (arm with floating point unit).
Required dependencies¶
Using python-deltasigma requires Python 2 or 3,
at your choice, numpy,
scipy (>= 0.11.0) and
matplotlib.
They are packaged by virtually all the major Linux distributions.
On a Debian Linux system, you may install them issuing:
aptitude install python python-numpy python-scipy python-matplotlib
Refer to your system documentation for more information.
On Windows, I hear good things about:
- Enthought Canopy, a Python distribution that carries both free and commercial versions, and
- Anaconda, which offers its full version for free.
I do not run Windows, so I can’t really provide more info (sorry), except that people tell me they manage to have a working setup.
Mac OS X is also supported by Enthought Canopy and Anaconda, which likely provide the easiest and fastest solution to have a scientific Python stack up and running.
More information can be found on the scipy install page and on the matplotlib homepage.
I wrote in a different context some directions to compile numpy and scipy yourself, which also apply here. Be warned, it can easily get complicated.
Optional (but recommended) dependencies¶
The required dependencies have been kept to a minimum to allow running
python-deltasigma on workstations that are not managed by the user
but by a system administrator - where typically installing libraries is
not possible and software packages are disarmingly outdated.
If at all possible, installing Cython is strongly recommended.
python-deltasigma contains python extension to simulate delta sigma
modulators providing a near-native execution speed – overall roughly a
70x speed-up compared to a plain Python implementation.
On Linux, installing Cython is just one: aptitude install cython away.
On Mac OS X and Windows, Cython may be installed as part of one of the frameworks above. Please notice a compiler is needed, this may require installing XCode and its command-line utilities or gcc through homebrew, on Mac OS X, or Mingw, on Windows.
If the BLAS headers are found on the machine, they will be used. In
case they cannot be found automatically, it is recommended to set
the environment variable BLAS_H to the BLAS headers directory.
On Mac OS X, consider linking the headers to their conventional location:
sudo ln -s /System/Library/Frameworks/Accelerate.framework/Versions/Current/Frameworks/vecLib.framework/Versions/Current/Headers/cblas.h /usr/include/cblas.h
The Cython extensions were written by Sergio Callegari, please see the
deltasigma/ for copyright notice and more information.
Install the deltasigma package¶
Once the dependencies set up, it is possible to install the latest stable version directly from the Python Package Index (PYPI), running:
pip install deltasigma
The above command will also attempt to compile and install the dependencies in case they are not found. Please notice this is not recommended and for this to work you should already have the required C libraries in place.
If you are interested in a bleeding-edge version – potentially less stable – or in contributing code (that’s awesome!) you can head over to the Github repository and check out the code from there.
Then run:
python setup.py install
The flag --user may be an interesting option to install the package for
the current user only, and it doesn’t require root privileges.
Extras for developers¶
The following may be installed at a later stage and are typically only necessary for developers.
Building the documentation requires the sphinx package. It is an optional step, as the the latest documentation is available on line, without need for you to build it.
If you plan to modify the code, python-deltasigma comes with a complete unit tests suite, which is run against every commit and that any addition should pass both for Python 2 and 3. To run it locally, setuptools is needed, as it is used to access the reference function outputs.
Running the test suite may be conveniently automated installing nose, and then issuing:
nosetests -v deltasigma
from the repository root.
Useful resources¶
The original MATLAB Toolbox provides in-depth documentation, which is very useful to understand what the toolbox is capable of. See DSToolbox.pdf and OnePageStory.pdf (PDF warning).
The book:
Richard Schreier, Gabor C. Temes, Understanding Delta-Sigma Data Converters, ISBN: 978-0-471-46585-0, November 2004, Wiley-IEEE Press
is probably the most authoritative resource on the topic. Chapter 8-9 show how to use the MATLAB toolkit and the observations apply also to this Python port. Links on amazon, on the Wiley-IEEE press.
I am not affiliated with neither the sellers nor the authors.
How to contribute¶
Pull requests are welcome!¶
If you want to port some code, fix a bug, add a cool example or implement new functionality (in this case it may be a good idea to get in touch early on), that’s awesome!
There are only a few guidelines, which can be overridden every time it is reasonable to do so:
- Please try to follow
PEP8. - Try to keep the functions signature identical. Parameters with
NaNdefault values have their default value replaced withNone. - If a function has a variable number of return values, its Python port should implement the maximum number of return values.
No commit should ever fail the test suite.
Reporting bugs¶
What bugs, there are no bugs!
Jokes aside, please report all bugs on on the Github issue tracker.
Support python-deltasigma¶
I do not want your money. I develop this software because I enjoy it and because I use it myself.
If you wish to support the development of python-deltasigma or you
find the package useful or you otherwise wish to contribute monetarily,
*please donate to cancer research instead:*
- Association for International Cancer Research (eng), or
- Fond. IRCCS Istituto Nazionale dei Tumori (it).
Consider sending me a mail afterwards, *it makes for great motivation!*
License, copyright, rationale and credits¶
Why this project was born¶
I like challenges, delta-sigma modulation and I don’t have the money for my own MATLAB license. After all, which grad student or young researcher has it?
With this Python package you can simulate delta-sigma modulators for free, on any PC.
I hope you find it useful.
Licensing and copyright notice¶
All original MATLAB code is Copyright (c) 2009, Richard Schreier. See the LICENSE file for the licensing terms.
The Python code here provided is a derivative work from the above toolkit and subject to the same license terms.
Credit goes to Richard Schreier for the original ideas, their MATLAB implementation and the all the diagrams found in this documentation. Little-to-no conceptual improvements are introduced here, just code adaptation, refactoring, rewrites and fixing of a few minor issues.
This package contains some source code from pydsm, also based on the
same MATLAB toolbox. The pydsm package is copyright (c) 2012, Sergio
Callegari.
When not otherwise specified, the Python code is Copyright 2013, Giuseppe Venturini and the python-deltasigma contributors.
MATLAB is a registered trademark of The MathWorks, Inc.
Credits¶
The python-deltasigma package was written by
Giuseppe Venturini, as a derivative work
of Richard Schreier’s MATLAB Delta Sigma toolbox. It contains code from
pydsm, also based on the same MATLAB toolbox and written by Sergio
Callegari.
Contributors: Shayne Hodge
Implementation model¶
The internal implementation of delta sigma modulators follows closely the one in Richard Schreier’s MATLAB Delta Sigma Toolbox, upon which the following documentation is very heavily based.
Modulator model¶
A delta-sigma modulator with a single quantizer is assumed to consist of quantizer connected to a loop filter as shown in the diagram below.

The loop filter¶
The loop filter is described by an \(ABCD\) matrix. For single-quantizer systems, the loop filter is a two-input, one-output linear system and \(ABCD\) is an \((n+1, n+2)\) matrix, partitioned into \(A\) \((n, n)\), \(B\) \((n, 2)\), \(C\) \((1, n)\) and \(D\) \((1, 2)\) sub-matrices as shown below:
The equations for updating the state and computing the output of the loop filter are:
Where \(u(n)\) is the input sequence and \(v(n)\) is the modulator output sequence.
This formulation is sufficiently general to encompass all single-quantizer modulators which employ linear loop filters. The toolbox currently supports translation to/from an ABCD descrip- tion and coefficients for the following topologies:
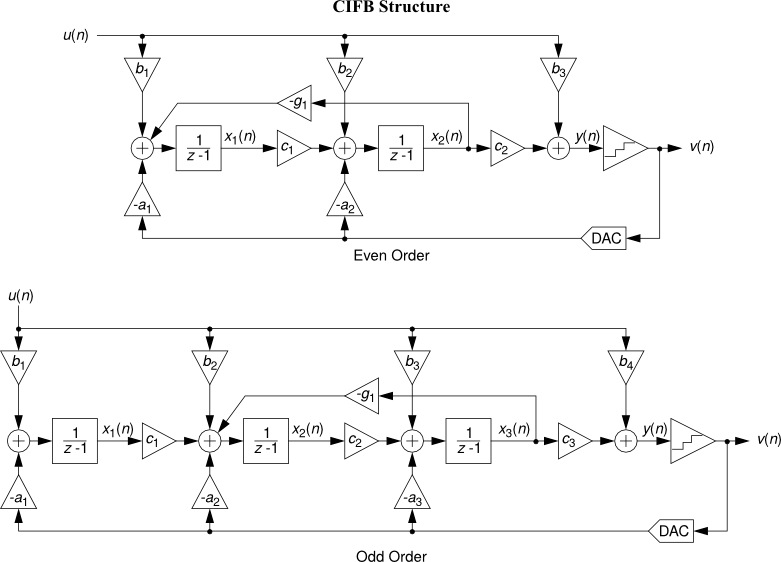
- CIFB : Cascade-of-integrators, feedback form.
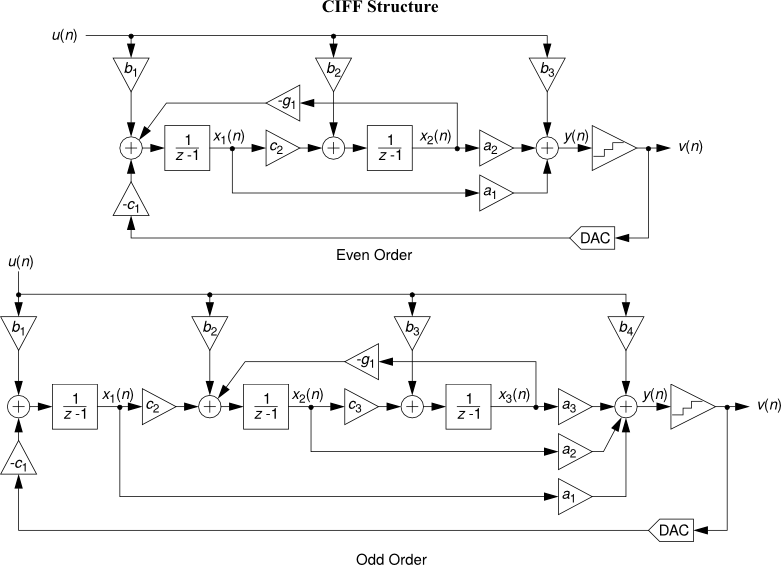
- CIFF : Cascade-of-integrators, feedforward form.
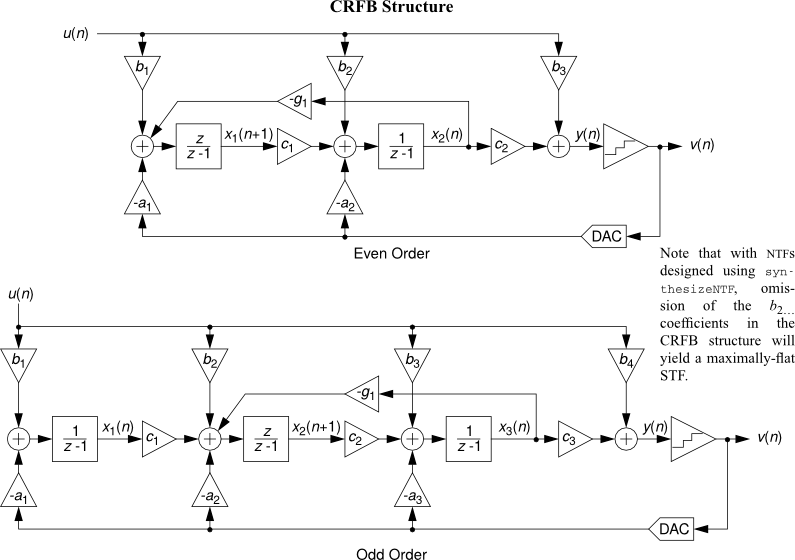
- CRFB : Cascade-of-resonators, feedback form.
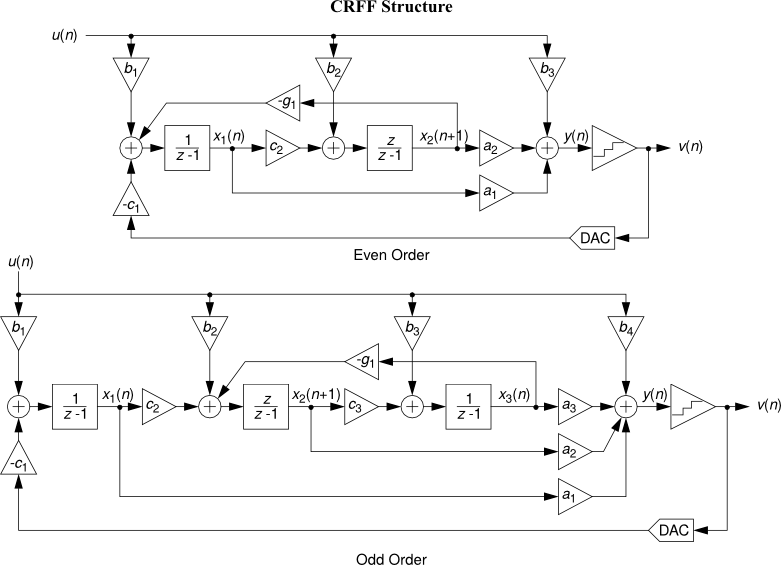
- CRFF : Cascade-of-resonators, feedforward form.
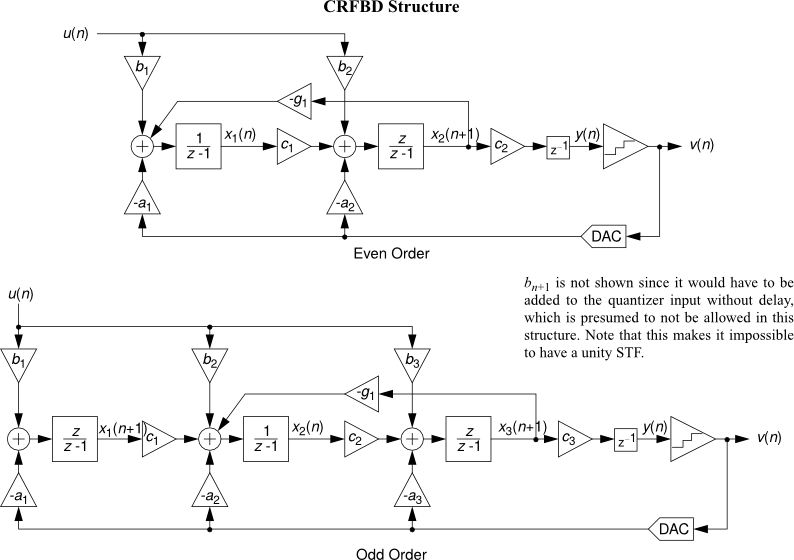
- CRFBD : Cascade-of-resonators, feedback form, delaying quantizer.
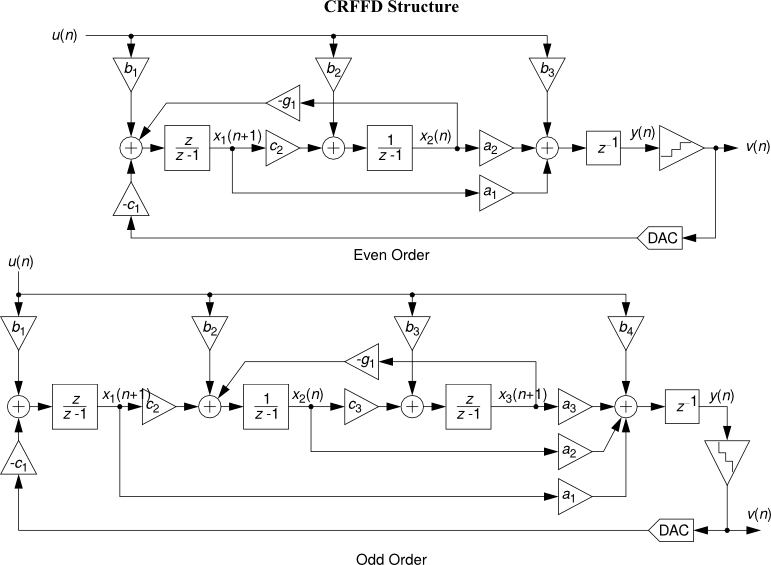
- CRFFD : Cascade-of-resonators, feedforward form, delaying quantizer
- PFF : Parallel feed-forward
- Stratos : A CIFF-like structure with non-delaying resonator feedbacks [*]
| [*] | Contributed to the MATLAB delta sigma toolbox in 2007 by Jeff Gealow. |
See Topologies diagrams for a block-level view of the different modulator structures.
Multi-input and multi-quantizer systems can also be described with an ABCD matrix and the previous equation will still apply. For an \(n_i\)-input, \(n_o\)-output modulator, the dimensions of the sub-matrices are \(A\): \((n, n)\), \(B\): \((n, n_i + n_o)\), \(C\): \((n_o, n)\) and \(D\): \((n_o, n_i+n_o)\).
Quantizer model¶
The quantizer is ideal, producing integer outputs centered about zero. Quantizers with an even number of levels are of the mid-rise type and produce outputs which are odd integers. Quantizers with an odd number of levels are of the mid-tread type and produce outputs which are even integers.

See also
Topologies diagrams¶
All the following topology diagrams are reproduced from DSToolbox.pdf in the MATLAB Delta Sigma Toolbox, written by Richard Schreier. All credits belong to the original author.
Discrete time to continuous time mapping¶
The approach presented here to design a CT delta-sigma modulator starts with the synthesis of the noise transfer function.
Once a suitable NTF has been identified, we need to realize the transfer function with a continuous time loop filter.
First, a loop filter topology is selected among the Feed-Forward (FF) and Feedback (FB) structures. The feed-forward or feedback paths – depending on the topology – will be characterized by an unknown proportionality factor \(k_i\), for each of the \(i \in \{0 \dots order\}\) branches.
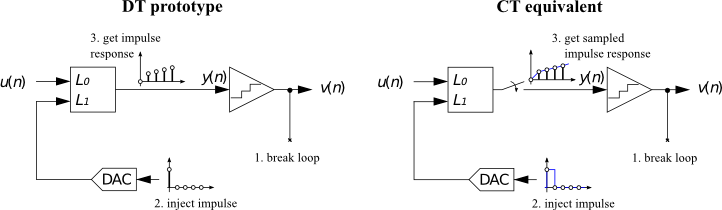
The objective is to determine the gain factors \({k_i}\) to construct a CT loop filter such that its sampled pulse response is equal to the impulse response of a DT prototype’s loop filter.
We consider here three approaches:
- equating the loop filter transfer functions,
- matching the loop filter impulse responses, implemented in
realizeNTF_ct()as method'LOOP', - matching the DT NTF and CT filter pulse responses, implemented in
realizeNTF_ct()as method'NTF'.
1: equate the loop filter transfer functions¶
The DT loop filter transfer function can be found from:
The CT loop filter is readily known, since it has been selected by the user, but it needs to be converted to an equivalent DT transformation. This operation is performed through the impulse invariance transformation, here denoted as \(\mathscr{I\!I\!T}\) [R2].
Solving the equation:
will allow determining the exact values of the coefficients \(k_i\) [R1].
This approach has limited use in the real case:
- Developing an analytical CT model and applying the impulse invariance transformation may entail significant difficulties in presence of non-idealities.
- The equation above will not have a solution when the integrators are non-ideal since the poles of the transfer functions on RHS and LHS are different.
2: match the loop filter impulse responses¶
Although it may be non-trivial to reach an analytical expression for \(\mathscr{I\!I\!T}\!\!\left(L_{1, CT}\right)(z)\), it is still possible to evaluate through numerical simulations (or in a some case analytically), N samples of the pulse response of each path \(\{l_i[n]\}\), obtained setting all the gain coefficients to one or \(k_i = 1, \; \forall i \in \{0 \dots order\}\).
Evaluating the impulse response of the prototype DT loop filter, denoted in the following as \(l[n]\), it is possible to write the equation:
Where we define the vector \(K\) as:
In the ideal case, provided that the impulse responses have been evaluated for a sufficiently high number of points \(N\) (\(N > order\)), the equation has a exact solution, independently of \(N\) [R2].
In presence of non-idealities, it is possible to use Least Squares fitting to find the optimum \(\{k_i\}\).
As discussed in [R3], this method is particularly sensitive to the value of \(N\) in the non-ideal cases.
3: match the DT NTF and CT filter pulse responses¶
A more robust approach is the following:
Remember the goal of DT to CT mapping is to have:
And by definition:
Combining the two we can write the equation:
To avoid having to apply the impulse invariance transformation, we can rewrite the above in the time domain, getting:
Where \(h[n]\) is the impulse response of the DT NTF.
The above can be rewritten as:
And solved exactly, in the ideal case, or in the least squares sense, in presence of non-idealities [R3].
| [R1] | P. Benabes, M. Keramat, and R. Kielbasa, “A methodology for designing continuous-time sigma-delta modulators,” in Proc. Eur. Conf. Design Test, Washington, DC, 1997, pp. 46-50 |
| [R2] | (1, 2) J. Cherry and W. Snelgrove, “Excess loop delay in continuous-time delta-sigma modulators,” IEEE Trans. Circuits Syst. II, Analog Digit. Signal Process., vol. 46, no. 4, pp. 376-389, Apr. 1999 |
| [R3] | (1, 2) Shanthi Pavan, “Systematic Design Centering of Continuous Time Oversampling Converters”, IEEE Trans. on Circuits Syst. II Express Briefs, Volume.57, Issue 3, pp.158, 2010 |
Package contents¶
Key Functions¶
synthesizeNTF() |
Synthesize a Noise Transfer Function (NTF) for a delta-sigma modulator. |
clans() |
Optimal NTF design for a multi-bit modulator. |
synthesizeChebyshevNTF() |
Synthesize a noise transfer function for a delta-sigma modulator. |
simulateDSM() |
Simulate a delta-sigma modulator. |
simulateSNR() |
Determine the SNR for a delta-sigma modulator by using simulations. |
realizeNTF() |
Convert an NTF into coefficients for the desired structure. |
stuffABCD() |
Calculate the ABCD matrix from the parameters of a modulator topology. |
mapABCD() |
Compute the coefficients for a given modulator topology. |
scaleABCD() |
Scale the loop filter of a general delta-sigma modulator for dynamic range. |
calculateTF() |
Calculate the NTF and STF of a delta-sigma modulator. |
realizeNTF_ct() |
Realize an NTF with a continuous-time loop filter. |
mapCtoD() |
Map a MIMO continuous-time modulator to an equivalent discrete-time counterpart. |
evalTFP() |
Evaluate a continuous-time - discrete-time transfer function product. |
Functions for quadrature delta-sigma modulators¶
Several of the previous functions also handle quadrature modulators.
In addition to those, the following are available specifically for quadrature modulators:
synthesizeQNTF() |
Synthesize a noise transfer function for a quadrature modulator. |
realizeQNTF() |
Convert a quadrature NTF into an ABCD matrix. |
simulateQDSM() |
Simulate a quadrature Delta-Sigma modulator. |
simulateQSNR() |
Determine the SNR for a quadrature delta-sigma modulator using simulations. |
calculateQTF() |
Calculate noise and signal transfer functions for a quadrature modulator. |
mapQtoR() |
Map a quadrature ABCD matrix to a real one. |
mapRtoQ() |
Map a real ABCD matrix to a quadrature one. |
Other selected functions¶
The following are auxiliary functions that complement the key functions above.
mod1() |
A description of the first-order modulator. |
mod2() |
A description of the second-order modulator. |
calculateSNR() |
Estimate the SNR from the FFT. |
predictSNR() |
Predict the SNR curve of a binary delta-sigma modulator. |
partitionABCD() |
Partition ABCD matrix into the state-space matrices A, B, C, D. |
infnorm() |
Find the infinity norm of a z-domain transfer function. |
impL1() |
Impulse response evaluation for NTFs. |
l1norm() |
Compute the l1-norm of a z-domain transfer function. |
pulse() |
Calculate the sampled pulse response of a CT system. |
rmsGain() |
Compute the root mean-square gain of a discrete-time TF. |
Utility functions for simulation of delta-sigma modulators¶
Functions for low-level handling of delta-sigma modulator representations, their evaluation and filtering.
bquantize() |
Bidirectionally quantize a 1D vector x to nsd signed digits. |
bunquantize() |
The value corresponding to a bidirectionally quantized quantity. |
delay() |
Delay a signal by a give number of samples. |
ds_f1f2() |
Get the neighboring frequencies to the carrier to calculate the SNR. |
ds_freq() |
Frequency vector suitable for plotting the frequency response of an NTF. |
ds_hann() |
A Hanning (Hann) window of given length. |
ds_quantize() |
Quantize a vector. |
dsclansNTF() |
Conversion of CLANS parameters into a NTF. |
evalMixedTF() |
Evaluate a mixed-signal transfer function. |
evalRPoly() |
Compute the value of a polynomial which is given in terms of its roots. |
evalTF() |
Evaluate the rational transfer function (TF) at the given z point(s). |
nabsH() |
Compute the negative of the absolute value of H. |
peakSNR() |
Find the SNR peak by fitting the SNR curve. |
sinc_decimate() |
Decimate a vector by a sinc filter of given order and length. |
zinc() |
Calculate the magnitude response of a cascade of n m-th order comb filters. |
General utilities for data processing¶
The following are functions useful for misc. tasks, like manipulating data, conversions or padding, for example. They provide specialty functions which are not otherwise available in the usual scientific Python stack.
circshift() |
Shift an array circularly. |
cplxpair() |
Sort complex roots into complex conjugate pairs. |
db() |
Calculate the dB equivalent of a given RMS signal. |
dbm() |
Calculate the dBm equivalent of a given RMS voltage. |
dbp() |
Calculate the dB equivalent of a given power ratio. |
dbv() |
Calculate the dB equivalent of a given voltage ratio. |
gcd() |
Calculate the Greatest Common Divisor (GCD) of two integers. |
lcm() |
Calculate the Least Common Multiple (LCD) of two integers. |
mfloor() |
Round a vector towards -Inf. |
mround() |
Round a vector to the nearest integers. |
padb() |
Pad a matrix on the bottom to length n with value val. |
padl() |
Pad a matrix on the left to length n with value val. |
padr() |
Pad a matrix on the right to length n with value val. |
padt() |
Pad a matrix on the top to length n with value val. |
rat() |
Rational fraction approximation. |
rms() |
Calculate the RMS value of x. |
undbm() |
Calculate the RMS voltage equivalent to a given power expressed in dBm. |
undbp() |
Calculate the power equivalent to a given value in dB. |
undbv() |
Calculate the voltage ratio equivalent to a given power expressed in dB. |
Plotting and data display utilities¶
Graphic functions:
DocumentNTF() |
Plot the NTF’s poles and zeros as well as its frequency-response. |
PlotExampleSpectrum() |
Plot a spectrum suitable to exemplify the NTF performance. |
axisLabels() |
Utility function to quickly generate the alphanumeric labels for a plot axis. |
bilogplot() |
Plot the spectrum of a band-pass modulator in dB. |
changeFig() |
Quickly change several figure parameters. |
figureMagic() |
Utility function to quickly set several plot parameters. |
lollipop() |
Plot lollipops (o’s and sticks). |
plotPZ() |
Plot the poles and zeros of a transfer function. |
plotSpectrum() |
Plot a smoothed spectrum on a LOG x-axis. |
Textual and non-graphic, display-related functions:
SIunits() |
Calculates the factor for representing a given value in engineering notation. |
bplogsmooth() |
Smooth the FFT and convert it to dB. |
circ_smooth() |
Smooth the PSD for linear x-axis plotting. |
logsmooth() |
Smooth the FFT, and convert it to dB. |
pretty_lti() |
A pretty representation of a TF, suitable for printing to screen. |
All functions in alphabetical order¶
-
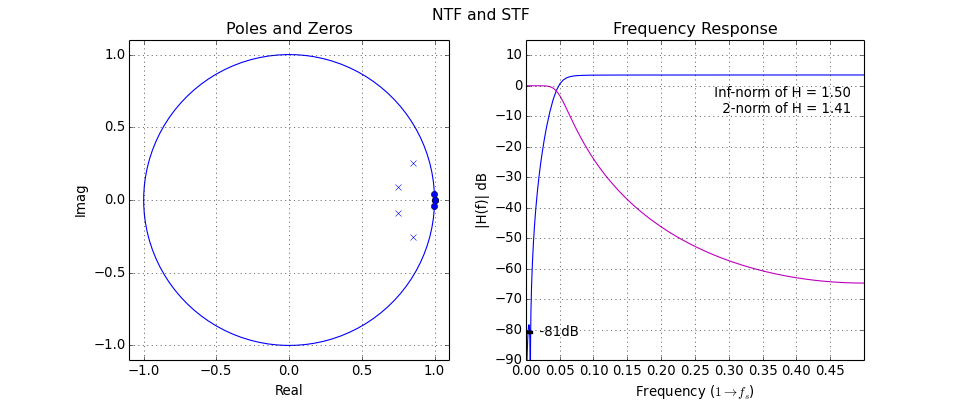
DocumentNTF(arg1, osr=64, f0=0, quadrature=False)[source]¶ Plot the NTF’s poles and zeros as well as its frequency-response
The first argument is either the NTF or ABCD matrix. If the first argument is ABCD, the STF is also plotted.
(Source code, png, hires.png, pdf)
-
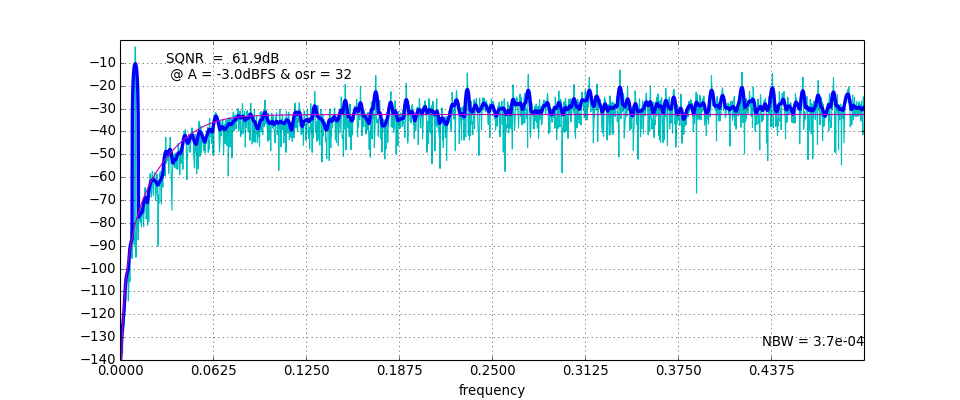
PlotExampleSpectrum(ntf, M=1, osr=64, f0=0, quadrature=False)[source]¶ Plot a spectrum suitable to exemplify the NTF performance.
Parameters:
- ntf : scipy ‘lti’ object, tuple or ndarray
- The first argument may be one of the various supported
representations for a (SISO) transfer function or an
ABCD matrix. See
evalTF()for a more detailed discussion. - f0 : float, optional
- The center frequency. Normalized. Defaults to 0.
- M : int, optional
M is defined as:
\[M = n_{lev} - 1\]The number of quantizer levels (\(n_{lev}\)) defaults to 2 and
Mdefaults to 1.- quadrature : boolean, optional
- Whether the delta sigma modulator is a quadrature
modulator or not. Defaults to
False.
(Source code, png, hires.png, pdf)
-
SIunits(x)[source]¶ Calculates the factor for representing
xin engineering notation.The factors and suffixes supported are:
1e-3 m milli 1e3 k kilo 1e-6 u micro 1e6 M mega 1e-9 n nano 1e9 G giga 1e-12 p pico 1e12 T tera 1e-15 f femto 1e15 P peta 1e-18 a atto 1e18 E exa 1e-21 z zepto 1e21 Z zeta 1e-24 y yocto 1e24 Y yotta Parameters:
- x : scalar or array_like
- The number for which the engineering notation factor and suffix
are to be calculated.
Returns:
- factor : float or list of floats
- the engineering notation factor(s)
- prefix : string or list of strings
- the engineering notation unit prefix(es)
Example:
a = 3300. unit = 'g' f, p = SIunits(a) print "Float 'a' in engineering notation: %.3f %s%s" % (a/f, p, unit)
Prints:
Float 'a' in engineering notation: 3.300 kg
-
axisLabels(ran, incr)[source]¶ Utility function to quickly generate the alphanum. axis labels.
Parameters:
- ran : sequence
- Sequence containing the axis points (floats)
- incr : int, or 2-elements sequence
- This parameter may be:
- an int, the function returns an array of strings corresponding to:
each element of
range[0]:range[-1]:incrformatted as'%g'. - a list, the function returns an array of strings corresponding to:
each element of
incr[1]:range[-1]:incr[0]formatted as'%g'.
Note
All elements in
ranless than 1e-6 are rounded down to 0.Returns:
labels : list of strings
Raises:
ValueError: “Unrecognised incr.”
-
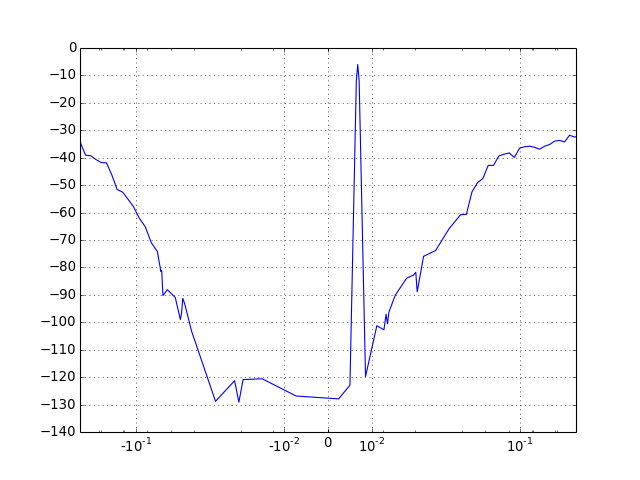
bilogplot(V, f0, fbin, x, y, **fmt)[source]¶ Plot the spectrum of a band-pass modulator in dB.
The plot is a logarithmic plot, centered in 0, corresponding to f0, extending to negative frequencies, with respect to the center frequencies and to positive frequencies.
The plot employs a logarithmic x-axis transform far from the origin and a linear one close to it, allowing the x-axis to reach zero and extend to negative values as well.
Note
This is implemented in a slightly different way from The MATLAB Delta Sigma Toolbox, where all values below
xminare clipped and the scale is always logarithmic. It our implementation, no clipping is done and belowxminthe data is simply plotted with a linear scale. For this reason slightly different plots may be generated.Parameters:
- V : 1d-ndarray or sequence
- Hann-windowed FFT
- f0 : int
- Bin number of center frequency
- fbin : int
- Bin number of test tone
- x : 3-elements sequence-like
- x is a sequence of three positive floats:
xmin,xmax_left,xmax_right.xminis the minimum value of the logarithmic plot range.xmax_leftis the length of the plotting interval on the left (negative) side,xmax_rightis its respective on the right (positive) side. - y : 3-elements sequence-like
- y is a sequence of three floats:
ymin,ymax,dy.yminis the minimum value of the y-axis,ymaxits maximum value anddyis the ticks spacing.
Note
The MATLAB Delta Sigma toolbox allows for a fourth option
y_skip, which is theincrvalue passed to MATLAB’saxisLabels. No such thing is supported here. A warning is issued iflen(v) == 4.Additional keyword parameters
**fmtwill be passed to matplotlib’ssemilogx().The FFT is smoothed before plotting and converted to dB. See
logsmooth()for details regarding the algorithm used.Returns:
None
(Source code, png, hires.png, pdf)
-
bplogsmooth(X, tbin, f0)[source]¶ Smooth the FFT and convert it to dB.
Use 8 bins from the bin corresponding to
f0totbinand again as far. Thereafter increase bin sizes by a factor of 1.1, staying less than 2^10. Fortbin, group the bins together.Use this for nice double-sided log-log plots.
Note
tbinis assumed to be in the upper sideband!See also
-
bquantize(x, nsd=3, abstol=2.2204460492503131e-16, reltol=2.2204460492503131e-15)[source]¶ Bidirectionally quantize a 1D vector
xtonsdsigned digits.This method will terminate early if the error is less than the specified tolerances.
The quantizer details are repeated here for the user’s convenience:
The quantizer is ideal, producing integer outputs centered about zero. Quantizers with an even number of levels are of the mid-rise type and produce outputs which are odd integers. Quantizers with an odd number of levels are of the mid-tread type and produce outputs which are even integers.

Parameters:
- x : array_like or sequence
- the data to be quantized.
- nsd : int, optional
- The number of signed digits.
- abstol and reltol : floats, optional
- If not supplied, the absolute tolerance and the relative
tolerance default to
epsand10*eps, resp.
Returns:
- y : list
- List of objects described below.
yis a list of instances with the same length asxand the following attributes:y[i].valis the quantized value in floating-point form,y[i].csdis a 2-by-nsd (or less) matrix containing the powers of two (first row) and their signs (second row).
See also
-
bunquantize(q)[source]¶ The value corresponding to a bidirectionally quantized quantity.
qis a (2n, m) ndarray containing the powers of 2 and their signs for each quantized value.See also
-
calculateSNR(hwfft, f, nsig=1)[source]¶ Estimate the SNR from the FFT.
Estimate the Signal-to-Noise Ratio (SNR), given the in-band bins of a Hann-windowed FFT and the location
f0of the input signal (f>0). Fornsig = 1, the input tone is contained inhwfft(f:f+2), this range is appropriate for a Hann-windowed FFT.Each increment in
nsigadds a bin to either side.The SNR is expressed in dB.
Parameters:
- hwfft : sequence
- the FFT
- f : integer
- Location of the input signal. Normalized.
Note
f = 0 corresponds to DC, as Python indexing starts from 0.
- nsig : integer, optional
- Extra bins added to either side. Defaults to 1.
Returns:
- SNR : scalar
- The computed SNR value in dB.
-
calculateTF(ABCD, k=1.0)[source]¶ Calculate the NTF and STF of a delta-sigma modulator.
The calculation is performed for a given loop filter ABCD matrix, assuming a quantizer gain of
k.Parameters:
- ABCD : array_like,
- The ABCD matrix that describes the system.
- k : float or ndarray-like, optional
- The quantizer gains. If only one quantizer is present, it may be set
to a float, corresponding to the quantizer gain. If multiple quantizers
are present, a list should be used, with quantizer gains ordered
according to the order in which the quantizer inputs appear in the
CandDsubmatrices. If not specified, a default of one quantizer with gain1.is assumed.
Returns:
- (NTF, STF) : a tuple of two LTI objects (or of two lists of LTI objects).
- If a version of the
scipylibrary equal to 0.16.x or greater is in use, the objects will beZeroPolesGainobjects, a subclass ofscipy.signal.lti.
If the system has multiple quantizers, multiple STFs and NTFs will be returned.
In that case:
STF[i]is the STF fromuto output numberi.NTF[i, j]is the NTF from the quantization noise of the quantizer numberjto output numberi.
Note:
Setting
kto a list is unsupported in the MATLAB code (last checked Nov. 2014).Example:
Realize a fifth-order modulator with the cascade-of-resonators structure, feedback form. Calculate the ABCD matrix of the loop filter and verify that the NTF and STF are correct.
from deltasigma import * H = synthesizeNTF(5, 32, 1) a, g, b, c = realizeNTF(H) ABCD = stuffABCD(a,g,b,c) ntf, stf = calculateTF(ABCD)
From which we get:
H:(z -1) (z^2 -1.997z +1) (z^2 -1.992z +0.9999) -------------------------------------------------------- (z -0.7778) (z^2 -1.796z +0.8549) (z^2 -1.613z +0.665)
coefficients:
a: 0.0007, 0.0084, 0.055, 0.2443, 0.5579 g: 0.0028, 0.0079 b: 0.0007, 0.0084, 0.055, 0.2443, 0.5579, 1.0 c: 1.0, 1.0, 1.0, 1.0, 1.0
ABCD matrix:
[[ 1.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 6.75559806e-04 -6.75559806e-04] [ 1.00000000e+00 1.00000000e+00 -2.79396240e-03 0.00000000e+00 0.00000000e+00 8.37752565e-03 -8.37752565e-03] [ 1.00000000e+00 1.00000000e+00 9.97206038e-01 0.00000000e+00 0.00000000e+00 6.33294166e-02 -6.33294166e-02] [ 0.00000000e+00 0.00000000e+00 1.00000000e+00 1.00000000e+00 -7.90937431e-03 2.44344030e-01 -2.44344030e-01] [ 0.00000000e+00 0.00000000e+00 1.00000000e+00 1.00000000e+00 9.92090626e-01 8.02273699e-01 -8.02273699e-01] [ 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 1.00000000e+00 1.00000000e+00 0.00000000e+00]]NTF:
(z -1) (z^2 -1.997z +1) (z^2 -1.992z +0.9999) -------------------------------------------------------- (z -0.7778) (z^2 -1.796z +0.8549) (z^2 -1.613z +0.665)
STF:
1
-
calculateQTF(ABCDr)[source]¶ Calculate noise and signal transfer functions for a quadrature modulator
Parameters:
- ABCDr : ndarray
- The ABCD matrix, in real form. You may call
mapQtoR()to convert an imaginary (quadrature) ABCD matrix to a real one.
Returns:
- ntf, stf, intf, istf : tuple of zpk tuples
- The quadrature noise and signal transfer functions.
Raises: RuntimeError – if the supplied ABCD matrix results in denominator mismatches.
-
cancelPZ(arg1, tol=1e-06)[source]¶ Cancel zeros/poles in a SISO transfer function.
Parameters:
- arg1 : LTI system description
Multiple descriptions are supported for the LTI system.
If one argument is used, it is a scipy
ltiobject.If more arguments are used, they should be arranged in a tuple, the following gives the number of elements in the tuple and their interpretation:
- 2: (numerator, denominator)
- 3: (zeros, poles, gain)
- 4: (A, B, C, D)
Each argument can be an array or sequence.
- tol : float, optional
- the absolute tolerance for pole, zero cancellation. Defaults to 1e-6.
Returns:
- (z, p, k) : tuple
- A tuple containing zeros, poles and gain (unchanged) after poles, zeros cancellation.
-
changeFig(fontsize=None, linewidth=None, markersize=None, xfticks=False, yfticks=False, bw=False, fig=None)[source]¶ Quickly change several figure parameters.
This function sweeps through all axes in the figure, and for each line and text item sets the line width, marker size, font size and the other parameters, if set.
All parameters that are unset are left untouched.
Parameters:
- fontsize : scalar, optional
- the font size, given in points, defaults to
None, no change. - linewidth : scalar, optional
- the line width, given in points. Defaults to
None, no change. - markersize : scalar, optional
- the marker size, given in points. Defaults to
None, no change. - xfticks : string, optional
this parameter may be set to
'sci'or'plain'and only has an effect on linear axes.If set to
'sci', the x-axis labels will be formatted in scientific notation, with three decimals, eg'1.000E3'. If set to plain, plain float formatting will be used, eg.'0.001'.Defaults to
None, meaning no change is performed.- yfticks : string, optional
this parameter may be set to
'sci'or'plain'and only has an effect on linear axes.If set to
'sci', the y-axis labels will be formatted in scientific notation, with three decimals, eg'1.000E3'. If set to plain, plain float formatting will be used, eg.'0.001'.Defaults to
None, meaning no change is performed.- bw : boolean, optional
- if set to
True, the figure will be converted to BW. Defaults toFalse. - fig : a matplotlib figure object, optional
- the figure to apply the modifications to, if not given, it is assumed to be the currently active figure.
Returns:
None.
Note
This function may be useful to enhance the readability of figures to be used in presentations.
See also
figureMagic(), to quickly change plot ranges and more.
-
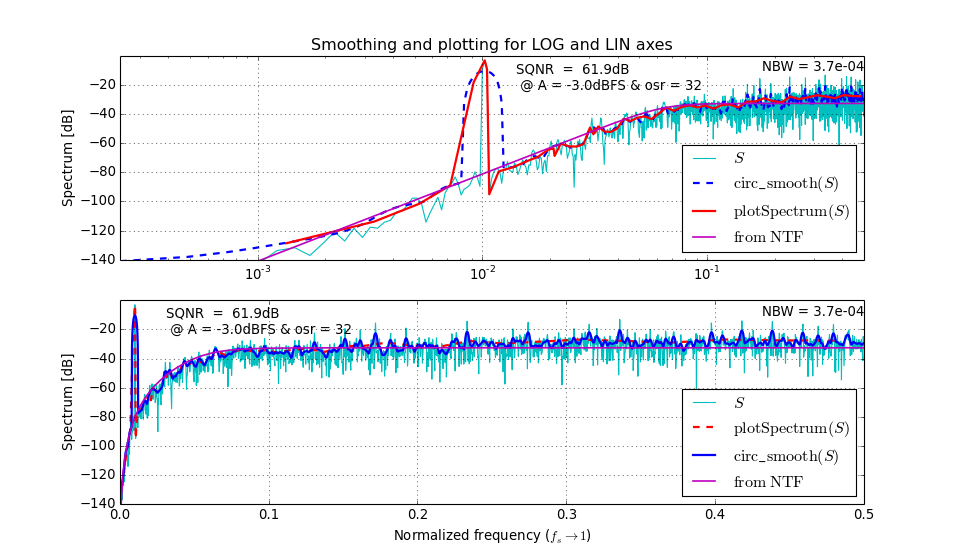
circ_smooth(x, n=16)[source]¶ Smoothing of the PSD
xfor linear x-axis plotting.Parameters:
- x : 1D ndarray
- The PSD to be smoothed, or equivalently
\[x = \left|\mathrm{FFT}\left(u(t)\right)(f)\right|^2\]- n : int, even, optional
- The length of the Hann window used in the smoothing algorithm.
Returns:
- y : 1D ndarray
- The smoothed PSD
See also
logsmooth(), smoothing algorithm suitable for logarithmic x-axis plotting.For a comparison of
circ_smooth()andlogsmooth()(accessed through the helper functionplotSpectrum()) see the following plot.(Source code, png, hires.png, pdf)
-
circshift(a, shift)[source]¶ Shift an array circularly.
The
circshift(a, shift)function circularly shifts the values in the arrayabyshiftelements.Parameters:
- a : ndarray
- the array to be shifted. Notice that a should have a greater or equal
number of dimensions than
shift(shiftbeing a scalar is equal toshiftbeing a one-dimension array.) - shift : int or ndarray-like of int.
- the N-th element specifies the shift amount for the N-th dimension
of the input array
a.
If an element in
shiftis positive, the values ofaare shifted to higher-index rows (ie down) or to higher-index columns (ie to the right).If the element is negative, the values of
aare shifted in the opposite directions, towards lower-index rows (ie up) or to lower-index columns (ie right).If
shiftis an integer, the shift happens along axis 0.All dimensions that do not have a corresponding shift value in
shiftare left untouched (ieshift=(1, 0, 0)is equal toshift=(1,), with the exception that the former will trigger anIndexErrorifa.ndim < 3).Returns:
The shifted array.
-
clans(order=4, OSR=64, Q=5, rmax=0.95, opt=0)[source]¶ Optimal NTF design for a multi-bit modulator.
Synthesize a noise transfer function (NTF) for a lowpass delta-sigma modulator using the CLANS methodology.
CLANS stands for Closed-Loop Analysis of Noise-Shapers, and it was originally developed by J.G. Kenney and L.R. Carley [1].
[1] J. G. Kenney and L. R. Carley, “Design of multibit noise-shaping data converters,” Analog Integrated Circuits Signal Processing Journal, vol. 3, pp. 259-272, 1993. Parameters:
- order : int
- The order of the NTF.
- OSR : int
- The oversampling ratio.
- Q : int
- The maximum number of quantization levels used by the fed-back quantization noise. (Mathematically, \(Q = \|h\|_1 - 1\), i.e. the sum of the absolute values of the impulse response samples minus one is the maximum instantaneous noise gain.)
- rmax : float
- The maximum radius for the NTF poles.
- opt : int
- A flag used to request optimized NTF zeros.
- opt=0 puts all NTF zeros at band center (DC for lowpass modulators).
- opt=1 optimizes the NTF zeros.
- For even-order modulators, opt=2 puts two zeros at band-center, but optimizes the rest.
Returns
- ntf : tuple
- The modulator NTF, given in ZPK (zero-pole-gain) form.
Example:
Fifth-order lowpass modulator; (time-domain) noise gain of 5, zeros optimized for OSR = 32.:
H = clans(5, 32, 5, .95, 1) pretty_lti(H)
Returns:
(z -1) (z^2 -1.997z +1) (z^2 -1.992z +0.9999) --------------------------------------------------------- (z -0.4184) (z^2 -1.305z +0.5713) (z^2 -0.978z +0.2686)
Hcan be plotted throughDocumentNTF():(Source code, png, hires.png, pdf)
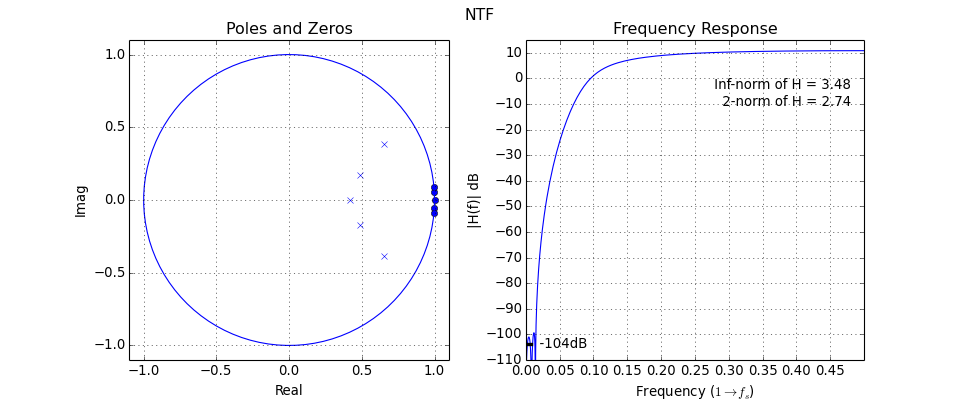
-
db(x, input_type='voltage', R=1.0)[source]¶ Calculate the dB equivalent of the RMS signal
x.For input type
"voltage", the return value is defined as\[P_{dB} = 20 \mathrm{log}_{10}\left(\frac{x}{R}\right)\]Otherwise, for input type
"power",\[P_{dB} = 10 \mathrm{log}_{10}(x)\]Parameters:
- x : scalar or sequence
- The signal to be converted.
- input_type : string, optional
- The input type, either
"voltage"or"power". - R : float, optional
- The normalization resistor value, used only for voltage inputs.
Returns:
- PdB : scalar or sequence
- The input expressed in dB.
Note
MATLAB provides a function with this exact signature.
-
dbm(v, R=50)[source]¶ Calculate the dBm equivalent of an RMS voltage
v.\[P_{dBm} = 10 \mathrm{log}_{10}(1000 \frac{v^2}{R} )\]Parameters:
- v : scalar or sequence
- The voltages to be converted.
- R : scalar, optional
- The resistor value the power is calculated upon, defaults to 50 ohm.
Returns:
- PdBm : scalar or sequence
- The input in dBm.
-
dbp(x)[source]¶ Calculate the dB equivalent of the power ratio
x.\[P_{dB} = 10 \mathrm{log}_{10}(x)\]Parameters:
- x : scalar or sequence
- The power ratio to be converted.
Returns:
- PdB : scalar or sequence
- The input expressed in dB.
-
dbv(x)[source]¶ Calculate the dB equivalent of the voltage ratio
x.\[G_{dB} = 20 \mathrm{log}_{10}(|x|)\]Parameters:
- x : scalar or sequence
- The voltage (ratio) to be converted.
Returns:
- GdB : scalar or sequence
- The input voltage (ratio) expressed in dB.
-
ds_f1f2(OSR=64, f0=0.0, complex_flag=False)[source]¶ [f1, f2] = ds_f1f2(OSR=64, f0=0, complex_flag=0) This function has no original docstring.
-
ds_freq(osr=64.0, f0=0.0, quadrature=False)[source]¶ Frequency vector suitable for plotting the frequency response of an NTF
-
ds_hann(n)[source]¶ A Hann window of length \(n\).
The Hann window, aka the raised cosine window, is defined as:
\[w(x) = 0.5\ \left(1 - cos\left(\frac{2 \pi x}{n}\right) \right)\]This windowing function does not smear tones located exactly in a bin.
Parameters:
- n : integer
- The window length, in number of samples.
Returns:
- w : 1d nd_array
- The Hann window.
Note
Functionally equivalent to numpy’s
hanning(), provided to ease porting of code from MATLAB. Also, we take care always to return an array of dimensions(n,)and typefloat_.(Source code, png, hires.png, pdf)
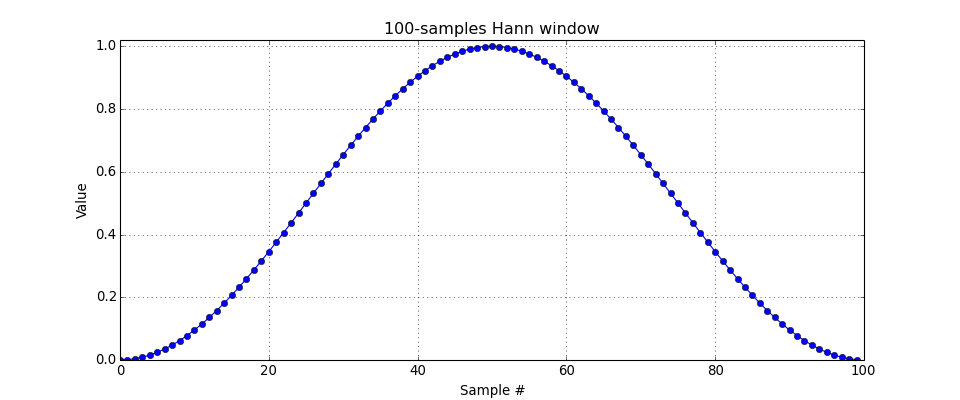
-
ds_optzeros(n, opt=1)[source]¶ A helper function for
synthesizeNTF()Returns the zeros which minimize the in-band noise power of a delta-sigma modulator’s NTF.
This function is not intended for direct use, but it is available for compliance with the Matlab Toolbox interface.
Parameters:
- n : int
- The order of the modulator
- opt : int
- A flag which selects the kind of optimization to be employed
for the zeros. A description of the possible values can be found
in the doc for
synthesizeNTF().
Returns:
- zeros : 1d-ndarray
- An array with the location of the zeros in the z plane, according to the specified optimization.
-
ds_quantize(y, n=2)[source]¶ Quantize
yQuantize a vector \(y\) to:
- an odd integer in \([-n+1, n-1]\), if \(n\) is even, or
- an even integer in \([-n+1, n-1]\), if \(n\) is odd.
The quantizer implementation details are repeated here from its documentation for the user’s convenience:
The quantizer is ideal, producing integer outputs centered about zero. Quantizers with an even number of levels are of the mid-rise type and produce outputs which are odd integers. Quantizers with an odd number of levels are of the mid-tread type and produce outputs which are even integers.This definition gives the same step height for both mid-rise and mid-tread quantizers.

Parameters:
- n : int or ndarray, optional
- The number of levels in the quantizer. If
nis an integer, then all rows of y are fed to the same quantizer. Ifnis a column vector, each of its elements specifies how to quantize the rows ofy.
Returns:
- v : ndarray
- The quantized vector.
See also
-
ds_synNTFobj1(x, p, osr, f0)[source]¶ Objective function for
synthesizeNTF()This function is not meant to be used directly but it is provided for compliance with the MATLAB DS Toolbox.
-
dsclansNTF(x, order, rmax, Hz)[source]¶ Conversion of clans parameters into a NTF.
Translate x into H. I’ve changed the relationships between (zeta, wn) and x in order to guarantee LHP roots of the s-polynomial.
Returns the NTF, a zpk tuple.
-
evalMixedTF(tf, f, df=1e-05)[source]¶ Compute a mixed transfer function.
Mathematically, it means to evaluate the sum of products:
\[TF(f) = \sum_i H_{z,i}(f) \cdot H_{s,i}(f)\]Parameters:
- tf : dict
tfis a dictionary of lists of 1d arrays, with keys ‘Hs’ and ‘Hz’, which represent continuous-time and discrete-time TFs which will be evaluated, multiplied together and then added up.- f : scalar or sequence-like
- The frequencies (or frequency, if
fis a scalar) at which the product will be evaluated. - df : float, optional
- If the method happens to evaluate a transfer function in a root, it
will move away of
df, defaulting to 1E-5.
Returns:
- TF : scalar or sequence
- The sum of products computed at
f.
-
evalRPoly(roots, x, k=1)[source]¶ Compute the value of a polynomial which is given in terms of its roots.
-
evalTF(tf, z)[source]¶ Evaluates the rational function
tfat the point(s) given inz.Parameters:
- tf : object
- the LTI description of the CT system, which can be in one of the following forms:
- an LTI object,
- a zpk tuple,
- a (num, den) tuple,
- an ABCD matrix (internally converted to zpk representation),
- a list-like containing the A, B, C, D matrices (also internally converted to zpk representation).
- z : scalar or 1d ndarray
- The z values for which
tfis to be evaluated.
Returns:
- tf(z) : scalar or 1d-ndarray
- The result.
-
evalTFP(Hs, Hz, f)[source]¶ Evaluate a CT-DT transfer function product.
Compute the value of a transfer function product Hs*Hz at a frequency f, where Hs is a continuous-time TF and Hz is a discrete-time TF.
Use this function to evaluate the signal transfer function of a continuous-time (CT) system. In this context
Hsis the open-loop response of the loop filter from theuinput andHzis the closed-loop noise transfer function.Note
This function attempts to cancel poles in
Hswith zeros inHz.Parameters:
- Hs : tuple
- Hs is a CT (SISO) TF in zpk-tuple form.
- Hz : tuple
- Hz is a DT (SISO) TF in zpk-tuple form.
- f : scalar or 1D array or sequence
- Frequency values.
Returns:
- H : scalar, or ndarray or sequence
The calculated values:
\[H(f) = H_s(j2\pi f)\ H_z(e^{j2\pi f})\]Hhas the same form asf.
See also
evalMixedTF(), a more advanced version of this function which is used to evaluate the individual feed-in transfer functions of a CT modulator.Example:
Plot the STF of the 2nd-order CT system depicted at
mapCtoD().:import numpy as np import pylab as plt from scipy.signal import lti from deltasigma import * from deltasigma._utils import _get_zpk Ac = np.array([[0, 0], [1, 0]]) Bc = np.array([[1, -1], [0, -1.5]]) Cc = np.array([[0, 1]]) Dc = np.array([[0, 0]]) LFc = (Ac, Bc, Cc, Dc) L0c = _get_zpk((Ac, Bc[:, 0].reshape((-1, 1)), Cc, Dc[0, 0].reshape(1, 1))) tdac = [0, 1] LF, Gp = mapCtoD(LFc, tdac) LF = lti(*LF) ABCD = np.vstack((np.hstack((LF.A, LF.B)), np.hstack((LF.C, LF.D)) )) H, _ = calculateTF(ABCD) # Yields H=(1-z^-1)^2 f = np.linspace(0, 2, 300); STF = evalTFP(L0c, _get_zpk(H), f) plt.figure(figsize=(12, 5)) plt.plot(f, dbv(STF)) plt.ylabel("|STF| [dB]") plt.xlabel("frequency ($1 \\rightarrow f_s$)") figureMagic((0, 2), .5, None, (-60, 0), 20, None)
(Source code, png, hires.png, pdf)
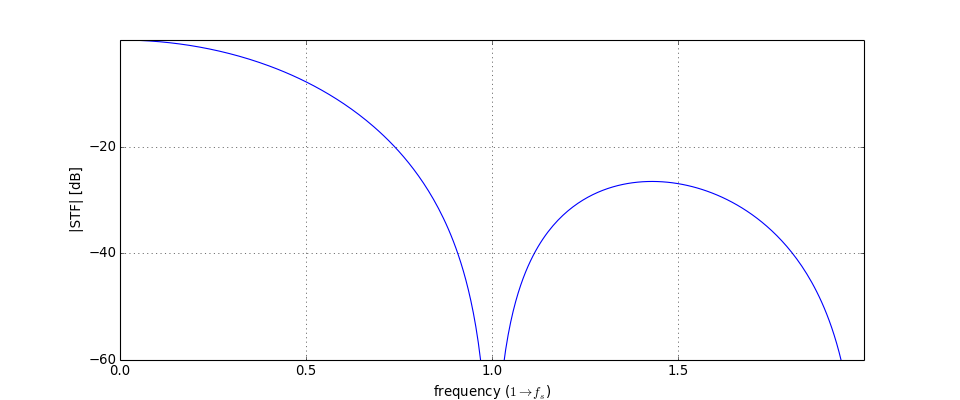
-
figureMagic(xRange=None, dx=None, xLab=None, yRange=None, dy=None, yLab=None, size=None, name=None)[source]¶ Utility function to quickly set plot parameters.
Parameters:
- xRange : 2 elements sequence, optional
- set the x-axis limits
- dx : scalar, optional
- set the ticks spacing on the x-axis
- xLab : any, optional
- Ignored variable, only accepted for compatibility with the MATLAB syntax.
- yRange : 2 elements sequence, optional
- set the y-axis limits
- dy : scalar, optional
- set the ticks spacing on the y-axis
- yLab : any, optional
- Ignored variable, only accepted for compatibility with the MATLAB syntax.
- size : 2-elements sequence, optional
- Figure size, in inches.
- name : string, optional
- Title for the current plot (or subplot)
All parameters are optional and any unspecified figure parameter is left untouched.
(Source code, png, hires.png, pdf)
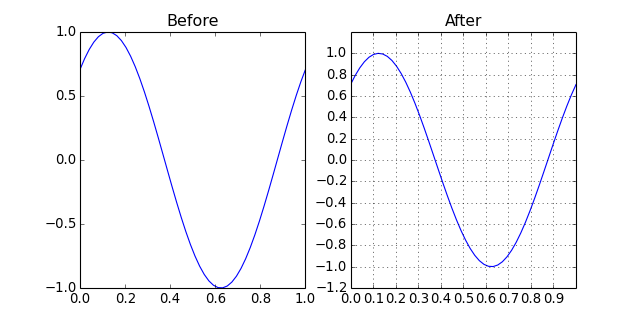
See also
changeFig()to quickly change low-level plot parameters such as font and marker size, the linewidth, or to prepare a plot for printing in B/W.
-
frespF1(f1, f=None, phi=1, plot=False)[source]¶ Plot/calculate the frequency response of the F1 filter in a Saramaki HBF at the points given in the optional f (n by 1) vector.
-
impL1(arg1, n=10)[source]¶ Impulse response evaluation for NTFs.
Compute the impulse response from the comparator output to the comparator input for the given NTF.
Parameters:
- arg1 : object
The NTF, which may be represented as:
- ZPK tuple,
- num, den tuple,
- A, B, C, D tuple,
- ABCD matrix,
- a scipy LTI object,
- a sequence of the tuples of any of the above types (experimental).
- n : int
- is the (optional) number of time steps (default: 10), resulting in an impulse response with n+1 (default: 11) samples.
This function is useful when verifying the realization of a NTF with a specified topology.
Returns:
- y : ndarray
- The NTF impulse response
Note
In the original implementation of impL1 in delsig, there is a bug: impL1 calls MATLAB’s impulse with tfinal=n, which means that the function will return the impulse response evaluated on the times [0, 1, 2 ... n], ie n+1 points. We keep the same behavior here, but we state clearly that n is the number of time steps.
-
infnorm(H)[source]¶ Find the infinity norm of a z-domain transfer function.
Parameters:
- H : object
the LTI description of the DT system, which can be in one of the following forms:
- an LTI object,
- a zpk tuple,
- a (num, den) tuple,
- an ABCD matrix (internally converted to zpk representation),
- a list-like containing the A, B, C, D matrices (also internally converted to zpk representation).
Returns:
- Hinf : float
- The infinity norm of
H. - fmax : float
- The frequency to which Hinf corresponds.
-
l1norm(H)[source]¶ Compute the l1-norm of a z-domain transfer function.
The norm is evaluated over the first 100 samples.
Parameters:
- H : sequence or lti object
- Any supported LTI representation is accepted.
Returns:
- l1normH : float
- The L1 norm of
H.
-
logsmooth(X, inBin, nbin=8, n=3)[source]¶ Smooth the FFT and convert it to dB.
Parameters:
- X : (N,) ndarray
- The FFT data.
- inBin : int
- The bin index of the input sine wave (if any).
- nbin : int, optional
- The number of bins on which the averaging will be performed, used before 3*inBin
- n : int, optional
- Around the location of the input signal and its harmonics (up to the third harmonic), don’t average for n bins.
The
logsmoothalgorithm usesnbinbins from 0 to 3*inBin, thereafter the bin sizes are increased by a factor 1.1, staying less than 2^10.For the \(n\) sets of bins: \(inBin + i, 2*inBin + i ... n*inBin+i\), where \(i \in [0,2]\) don’t do averaging. This way, the noise BW and the scaling of the tone and its harmonics are unchanged.
Note
Unfortunately, harmonics above the nth appear smaller than they really are because their energy is averaged over many bins.
Returns:
- f, p : tuple of 1d-arrays
- The bins and smoothed FFT, expressed in dB.
See also
plotSpectrum(), convenience function to first calllogsmooth()and then plot on a logarithmic x-axis its return values.circ_smooth(), smoothing algorithm suitable for linear x-axis plotting.
(Source code, png, hires.png, pdf)
-
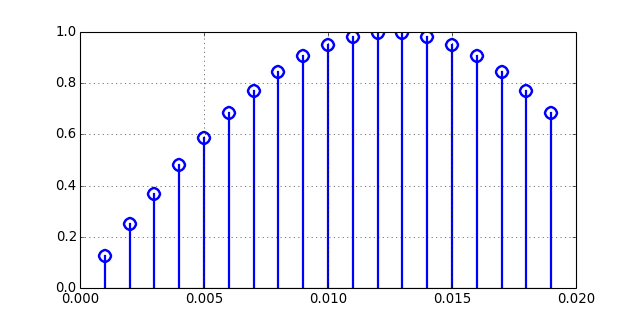
lollipop(x, y, color=None, lw=2, ybot=0)[source]¶ Plot lollipops (o’s and sticks)
Parameters:
- x, y : ndarrays
- The data to be plotted
- color : any matplotlib color, optional
- plotting color
- lw : float, optional
- line width value in points
- ybot : float, optional
- Dummy parameter available for compatibility
Returns:
None
Example:
(Source code, png, hires.png, pdf)
-
mapABCD(ABCD, form='CRFB')[source]¶ Compute the coefficients for the specified structure.
It is assumed that the ABCD matrix fits the topology.
Parameters:
- ABCD : ndarray
- A state-space description of the modulator loop filter.
- form : str, optional
- See
realizeNTF()for a list of supported structures.
Returns:
- a : ndarray
- Feedback/feedforward coefficients from/to the quantizer. Length \(n\).
- g : ndarray
- Resonator coefficients. Length \(floor(n/2)\).
- b : ndarray
- Feed-in coefficients from the modulator input to each integrator. Length \(n + 1\).
- c : ndarray
- Integrator inter-stage coefficients. Length \(n\).
See also
realizeNTF()for a list of supported structures.stuffABCD(), the inverse function.
-
mapCtoD(sys_c, t=(0, 1), f0=0.0)[source]¶ Map a MIMO continuous-time to an equiv. SIMO discrete-time system.
The criterion for equivalence is that the sampled pulse response of the CT system must be identical to the impulse response of the DT system. i.e. If
ycis the output of the CT system with an inputvctaken from a set of DACs fed with a single DT inputv, theny, the output of the equivalent DT system with inputvsatisfies:y(n) = yc(n-)for integern. The DACs are characterized by rectangular impulse responses with edge times specified in the t list.Input:
- sys_c : object
- the LTI description of the CT system, which can be:
- the ABCD matrix,
- a list-like containing the A, B, C, D matrices,
- a list of zpk tuples (internally converted to SS representation),
- a list of LTI objects.
- t : array_like
- The edge times of the DAC pulse used to make CT waveforms from DT inputs. Each row corresponds to one of the system inputs; [-1 -1] denotes a CT input. The default is [0 1], for all inputs except the first.
- f0 : float
- The (normalized) frequency at which the Gp filters’ gains are to be set to unity. Default 0 (DC).
Output:
- sys : tuple
- the LTI description for the DT equivalent, in A, B, C, D representation.
- Gp : list of lists
- the mixed CT/DT prefilters which form the samples fed to each state for the CT inputs.
Example:
Map the standard second order CT modulator shown below to its CT equivalent and verify that its NTF is \((1-z^{-1})^2\).

It can be done as follows:
from __future__ import print_function import numpy as np from scipy.signal import lti from deltasigma import * LFc = lti([[0, 0], [1, 0]], [[1, -1], [0, -1.5]], [[0, 1]], [[0, 0]]) tdac = [0, 1] LF, Gp = mapCtoD(LFc, tdac) LF = lti(*LF) ABCD = np.vstack(( np.hstack((LF.A, LF.B)), np.hstack((LF.C, LF.D)) )) NTF, STF = calculateTF(ABCD) print("NTF:") # after rounding to a 1e-6 resolution print("Zeros:", np.real_if_close(np.round(NTF.zeros, 6))) print("Poles:", np.real_if_close(np.round(NTF.poles, 6)))
Prints:
Zeros: [ 1. 1.] Poles: [ 0. 0.]
Equivalent to:
(z -1)^2 NTF = ---------- z^2See also
- Schreier and B. Zhang, “Delta-sigma modulators employing continuous-time circuitry,” IEEE Transactions on Circuits and Systems I, vol. 43, no. 4, pp. 324-332, April 1996.
-
mapQtoR(ABCD)[source]¶ Map a quadrature ABCD matrix to a real one.
Each element \(z\) in \(ABCD\) is replaced by a 2x2 matrix in
ABCDr, the return value.Specifically:
\[\begin{split}z \rightarrow \begin{bmatrix} x & -y \\ y & x \\ \end{bmatrix} \mathrm{where}\ x = Re(z)\ \mathrm{and}\ y = Im(z)\end{split}\]The non-quadrature topology then can be simulated with
simulateDSM().Example:
import numpy as np from deltasigma import * nlev = 9 f0 = 1./16. osr = 32 M = nlev - 1 ntf = synthesizeQNTF(4, osr, f0, -50, -10) N = 64*osr f = int(np.round((f0 + 0.3*0.5/osr)*N)/N) u = 0.5*M*np.exp(2j*np.pi*f*np.arange(N)) # Instead of calling simulateQDSM # v = simulateQDSM(u, ntf, nlev) # it's faster to run: ABCD = realizeQNTF(ntf, 'FF') ABCDr = mapQtoR(ABCD) ur = np.vstack((np.real(u), np.imag(u))) vr = simulateDSM(ur, ABCDr, nlev*np.array([[1],[1]])) v = vr[0,:] + 1j*vr[1, :]
Note
The scheme above often results in a shorter simulation time compared to calling
simulateQDSM()directly.
-
mapRtoQ(ABCDr)[source]¶ Map a real ABCD matrix to a quadrature one.
Parameters:
- ABCDr : ndarray
- A real matrix describing a quadrature system.
ABCDrhas its states paired (real, imaginary).Returns:
(ABCDq, ABCDp) : tuple
Where:
- ABCDq : ndarray
- is the quadrature (complex) version of ABCDr.
- ABCDp : ndarray
- is the mirror-image system matrix.
Note
ABCDpis zero ifABCDrhas no quadrature errors.
-
mod1()[source]¶ A description of the first-order modulator.
Returns:
- ABCD, NTF, STF : a tuple of (ndarray, lti, lti)
- The elements are the ABCD matrix (ndarray), the NTF (LTI object), the STF (LTI object).
Note
If a version of the
scipylibrary equal to 0.16.x or greater is in use, the NTF and STF objects will beZeroPolesGainobjects, a subclass of the scipy LTI object (scipy.signal.lti).
-
mod2()[source]¶ A description of the second-order modulator.
Returns:
- ABCD, NTF, STF : a tuple of (ndarray, lti, lti)
- The elements are the ABCD matrix (ndarray), the NTF (LTI object), the STF (LTI object).
Note
If a version of the
scipylibrary equal to 0.16.x or greater is in use, the NTF and STF objects will beZeroPolesGainobjects, a subclass of the scipy LTI object (scipy.signal.lti).
-
nabsH(w, H)[source]¶ Computes the negative of the absolute value of H.
The computation is performed at the specified angular frequency
w, on the unit circle.This function is used by
infnorm().
-
padb(x, n, val=0.0)[source]¶ Pad a matrix
xon the bottom to lengthnwith valueval.Parameters:
- x : ndarray
- The matrix to be padded.
- n : int
- The number of rows of the matrix after padding.
- val : scalar, optional
- The value to be used used for padding.
Note
A 1-d array, for example
a.shape == (N,)is reshaped to be a 1 column array:a.reshape((N, 1))The empty matrix is assumed to be have 1 empty column.
Returns:
- xp : 2-d ndarray
- The padded matrix.
-
padl(x, n, val=0.0)[source]¶ Pad a matrix
xon the left to lengthnwith valueval.Parameters:
- x : ndarray
- The matrix to be padded.
- n : int
- The number of columns of the matrix after padding.
- val : scalar, optional
- The value to be used used for padding.
Note
A 1-d array, for example
a.shape == (N,)is reshaped to be a 1 row array:a.reshape((1, N))The empty matrix is assumed to be have 1 empty row.
Returns:
- xp : 2-d ndarray
- The padded matrix.
-
padr(x, n, val=0.0)[source]¶ Pad a matrix
xon the right to lengthnwith valueval.Parameters:
- x : ndarray
- The matrix to be padded.
- n : int
- The number of columns of the matrix after padding.
- val : scalar, optional
- The value to be used used for padding.
Note
A 1-d array, for example
a.shape == (N,)is reshaped to be a 1 row array:a.reshape((1, N))The empty matrix is assumed to be have 1 empty row.
Returns:
- xp : 2-d ndarray
- The padded matrix.
-
padt(x, n, val=0.0)[source]¶ Pad a matrix
xon the top to lengthnwith valueval.Parameters:
- x : ndarray
- The matrix to be padded.
- n : int
- The number of rows of the matrix after padding.
- val : scalar, optional
- The value to be used used for padding.
Note
A 1-d array, for example
a.shape == (N,)is reshaped to be a 1 column array:a.reshape((N, 1))The empty matrix is assumed to be have 1 empty column.
Returns:
- xp : 2-d ndarray
- The padded matrix.
-
partitionABCD(ABCD, m=None, r=None)[source]¶ Partition ABCD into A, B, C, D for an m-input r-output system.
The \(ABCD\) matrix is defined as:
\[\begin{split}ABCD = \left[ \begin{array}{c|c} A & B \\ \hline C & D \end{array} \right].\end{split}\]The matrices \(A\), \(B\), \(C\) and \(D\) define the evolution of a generic linear discrete time invariant system under study through the state-space representation:
\[x(k + 1) = Ax(k) + Bu(k)\]\[y(k) = Cx(k) + Du(k)\]The matrices are:
- \(A\) is the state matrix, dimensions \((n, n)\), \(n\) being the number of states in the system,
- \(B\) is the input matrix, dimensions \((n, m)\), \(m\) being the number of inputs in the system,
- \(C\) is the output matrix, dimensions \((r, n)\), \(r\) being the number of outputs in the system,
- \(D\) is the feedthrough matrix, dimensions \((r, m)\).
The vectors are:
- \(x(k)\) the state sequence, of length \(n\),
- \(u(k)\), the input sequence, of length \(m\), and
- \(y(k)\) is the output sequence, of length \(r\).
Parameters:
- ABCD: ndarray
- The ABCD matrix to be partitioned
- m: int, optional
- The number of inputs in the system. It will be calculated from the ABCD matrix, if not provided.
- r: int, optional
- The number of outputs in the system. It will be calculated from
mand the ABCD matrix, if not provided.
Returns:
- A, B, C, D: tuple of ndarrays
- The partitioned matrices.
See also
Modulator model: loop filter for a discussion of the ABCD matrix in the particular case of a delta-sigma modulator loop filter.
-
peakSNR(snr, amp)[source]¶ Find the SNR peak by fitting the SNR curve.
A smooth curve is fitted to the top end of the SNR vs input amplitude data with Legendre’s least-squares method.
The curve fitted to the data is:
\[y = ax + \frac{b}{x - c}\]Parameters:
- snr : 1D ndarray or array-like
- Signal to Noise Ratio array, expressed in decibels (dB).
- amp : 1D ndarray or array-like
- Amplitude array, expressed in decibels (dB).
The two arrays
snrandampshould have the same size.Returns:
- (peak_snr, peak_amp) : tuple
- The peak SNR value and its corresponding amplitude, expressed in dB.
-
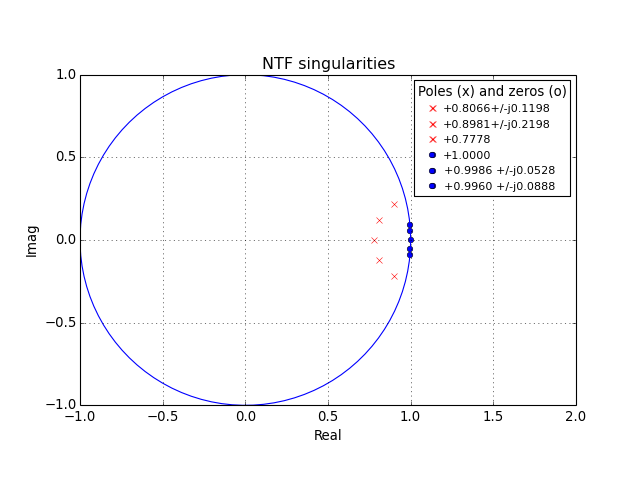
plotPZ(H, color='b', markersize=5, showlist=False)[source]¶ Plot the poles and zeros of a transfer function.
Parameters:
- H : transfer function
- Any supported transfer function representation, eg num/den, zpk, lti...
- color : Any matplotlib-compatible color descr, optional
- For example, ‘r’ for ‘red’ or ‘#000080’ for ‘navy’. You can also specify separately poles and zeros, in a tuple.
- markersize : scalar, optional
- The markers size in points.
- showlist : boolean, optional
- Superimpose a list of the poles and zeros on the plot.
(Source code, png, hires.png, pdf)
-
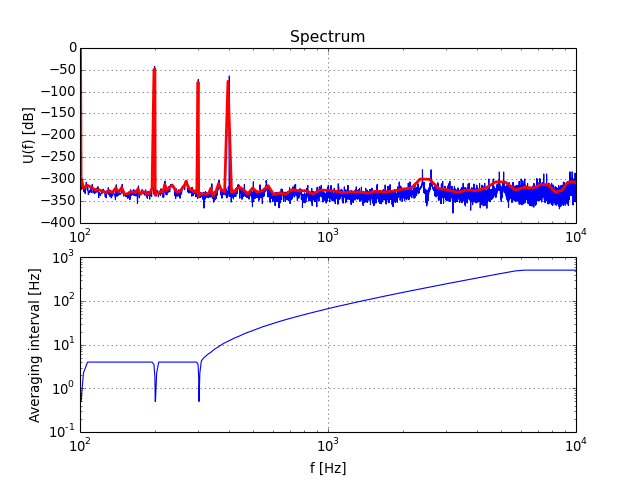
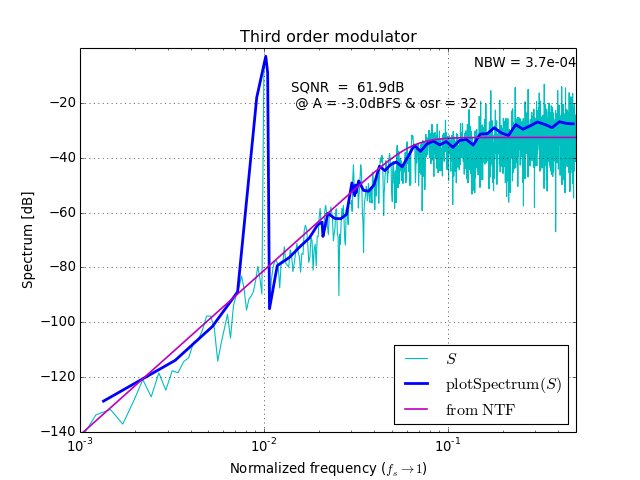
plotSpectrum(X, fin, fmt='-', **xargs)[source]¶ Plot a smoothed spectrum on a LOG x-axis.
Parameters:
- X : 1D ndarray
- The FFT to be smoothed and plotted, dual sided.
- fin : int
- The bin corresponding to the input sine wave.
- fmt : string, optional
- Formatting to be passed to matplotlib’s
semilogx(). - **xargs : dict, optional
- Extra arguments to be passed to matplotlib’s
semilogx().
Plotting is performed on the current figure.
See also
logsmooth()for more information on the smoothing algorithmcirc_smooth()for a smoothing algorithm suitable for linear x-axes.
(Source code, png, hires.png, pdf)
-
predictSNR(ntf, OSR=64, amp=None, f0=0.0)[source]¶ Predict the SNR curve of a binary delta-sigma modulator.
The prediction is performed using the describing function method of Ardalan and Paulos [2] .
Parameters:
- ntf : lti object, or zpk or (num, den) or (A,B,C,D) tuples
- The noise transfer function specifying the modulator.
- OSR : scalar, optional
- The oversampling ratio, defaults to 64.
- amp : ndarray-like, optional
- The magnitudes to be used for the input signal. They are expressed in dB, where 0 dB means a full-scale (peak value = 1) sine wave. Defaults to [-120 -110 ... -20 -15 -10 -9 -8 ... 0].
- f0 : scalar, optional
- The normalized input signal frequency. Defaults to 0.
Notes:
The band of interest is defined by the oversampling ratio (
OSR) and the center frequency (f0).The algorithm assumes that the
ampvector is sorted in increasing order; once instability is detected, the remaining SNR values are set to-Inf.Future versions may accommodate STFs.
Returns:
- snr : ndarray
- A vector of SNR values, in dB.
- amp : ndarray
- A vector of amplitudes, in dB.
- k0 : ndarray
- The quantizer signal gain.
- k1: ndarray
- The quantizer noise gain.
- sigma_e2 : scalar
- The power of the quantizer noise (not in dB).
Implementation details:
The describing function method of A&P treats the quantizer processes signal and noise components separately. The quantizer is modeled as two (not necessarily equal) linear gains, \(k_0\) (
k0in the code) and \(k_1\) (k1), and an additive white Gaussian noise source of power \(\sigma_e^2\) (sigma_e2), as shown in the figure below.\(k_0\), \(k_1\) and \(\sigma_e^2\) are calculated as functions of the input.

The modulator’s loop filter is assumed to have nearly infinite gain at the test frequency.
Example:
See
simulateSNR()for an example use of this function.References
[2] Ardalan, S.H.; Paulos, J.J., “An analysis of nonlinear behavior in delta - sigma modulators,” Circuits and Systems, IEEE Transactions on, vol.34, no.6, pp.593,603, Jun 1987
-
pulse(S, tp=(0.0, 1.0), dt=1.0, tfinal=10.0, nosum=False)[source]¶ Calculate the sampled pulse response of a CT system.
tpmay be an array of pulse timings, one for each input, or even a simple 2-elements tuple.Parameters:
- S : sequence
- A sequence of LTI objects specifying the system.
The sequence S should be assembled so that
S[i][j]returns the LTI system description from inputito the outputj.In the case of a MISO system, a unidimensional sequence
S[i]is also acceptable.- tp : array-like
- An (n, 2) array of pulse timings
- dt : scalar
- The time increment
- tfinal : scalar
- The time of the last desired sample
- nosum : bool
- A flag indicating that the responses are not to be summed
Returns:
- y : ndarray
- The pulse response
-
realizeNTF(ntf, form='CRFB', stf=None)[source]¶ Convert an NTF into coefficients for the desired structure.
Parameters:
- ntf : a zpk transfer function
- The modulator noise transfer function (NTF)
- form : string
- A structure identifier.
Supported structures are:
- “CRFB”: Cascade of resonators, feedback form.
- “CRFF”: Cascade of resonators, feedforward form.
- “CIFB”: Cascade of integrators, feedback form.
- “CIFF”: Cascade of integrators, feedforward form.
- “CRFBD”: CRFB with delaying quantizer.
- “CRFFD”: CRFF with delaying quantizer.
- “PFF”: Parallel feed-forward.
- “Stratos”: A CIFF-like structure with non-delaying resonator feedbacks, contributed to the MATLAB Delta Sigma toolbox in 2007 by Jeff Gealow.
See the accompanying documentation (Topologies diagrams) for block diagrams of each structure.
- stf : a zpk transfer function, optional
- the Signal Transfer Function
Returns:
- a, g, b, c : tuple of ndarrays
- the coefficients for the desired structure
Example:
Determine the coefficients for a 5th-order modulator with the cascade-of-resonators structure, feedback (CRFB) form.:
from deltasigma import synthesizeNTF, realizeNTF H = synthesizeNTF(5, 32, 1) a, g, b, c = realizeNTF(H,'CRFB')
Returns the values:
a: 0.0007, 0.0084, 0.055, 0.2443, 0.5579 g: 0.0028, 0.0079 b: 0.0007, 0.0084, 0.055, 0.2443, 0.5579, 1.0 c: 1.0, 1.0, 1.0, 1.0, 1.0
-
realizeNTF_ct(ntf, form='FB', tdac=(0, 1), ordering=None, bp=None, ABCDc=None, method='LOOP')[source]¶ Realize an NTF with a continuous-time loop filter.
Parameters:
- ntf : object
- A noise transfer function (NTF).
- form : str, optional
A string specifying the topology of the loop filter.
- ‘FB’: Feedback form,
- ‘FF’: Feedforward form
For the FB structure, the elements of
Bcare calculated so that the sampled pulse response matches the L1 impulse response. For the FF structure,Ccis calculated.- tdac : sequence, optional
The timing for the feedback DAC(s). If
tdac[0] >= 1, direct feedback terms are added to the quantizer.Multiple timings (one or more per integrator) for the FB topology can be specified by making tdac a list of lists, e.g.
tdac = [[1, 2], [1, 2], [[0.5, 1], [1, 1.5]], []]In this example, the first two integrators have DACs with
[1, 2]timing, the third has a pair of DACs, one with[0.5, 1]timing and the other with[1, 1.5]timing, and there is no direct feedback DAC to the quantizer.- ordering : sequence, optional
- A vector specifying which NTF zero-pair to use in each resonator Default is for the zero-pairs to be used in the order specified in the NTF.
- bp : sequence, optional
- A vector specifying which resonator sections are bandpass.
The default (
zeros(...)) is for all sections to be lowpass. - ABCDc : ndarray, optional
- The loop filter structure, in state-space form. If this argument is omitted, ABCDc is constructed according to “form.”
- method : str, optional
- The default fitting method is
'LOOP', which means that the DT and CT loop responses will be matched. Alternatively, it is possible to set the method to'NTF', which will result in the NTF responses to be matched. See Discrete time to continuous time mapping for a more in-depth discussion.
Returns:
- ABCDc : ndarray
- A state-space description of the CT loop filter
- tdac2 : ndarray
- A matrix with the DAC timings, including ones that were automatically added.
Example:
Realize the NTF \((1 - z^{-1})^2\) with a CT system (cf with the example at
mapCtoD()).:from deltasigma import * ntf = ([1, 1], [0, 0], 1) ABCDc, tdac2 = realizeNTF_ct(ntf, 'FB')
Returns:
ABCDc:
[[ 0. 0. 1. -1. ] [ 1. 0. 0. -1.49999999] [ 0. 1. 0. 0. ]]
tdac2:
[[-1. -1.] [ 0. 1.]]
-
realizeQNTF(ntf, form='FB', rot=False, bn=0.0)[source]¶ Convert a quadrature NTF into an ABCD matrix
The basic idea is to equate the value of the loop filter at a set of points in the z-plane to the values of \(L_1 = 1-1/H\) at those points.
The order of the zeros is used when mapping the NTF onto the chosen topology.
Supported structures are:
- ‘FB’: Feedback
- ‘PFB’: Parallel feedback
- ‘FF’: Feedforward (bn is the coefficient of the aux DAC)
- ‘PFF’: Parallel feedforward
Not currently supported - feel free to send in a patch:
- ‘FBD’: FB with delaying quantizer
- ‘FFD’: FF with delaying quantizer
Parameters:
- ntf : lti object or supported description
- The NTF to be converted.
- form : str, optional
- The form to be used. See above for the currently supported
topologies. Defaults to
'FB'. - rot : bool, optional
- Set
rottoTrueto rotate the states to make as many coefficients as possible real. - bn : float, optional
- Coefficient of the auxiliary DAC, to be specified for a
‘FF’ form. Defaults to
0.0.
Returns:
- ABCD : ndarray
- ABCD realization of the requested type.
-
rms(x, no_dc=False)[source]¶ Calculate the RMS value of
x.The Root Mean Square value of an array \(x\) of length \(n\) is defined as:
\[x_{RMS} = \sqrt{\frac{1}{n}(x_1^2 + x_2^2 + ...+x_n^2)}\]Parameters:
- x : (N,) ndarray
- The input vector
- no_dc : boolean, optional
- If set to
True, the DC value gets subtracted fromxfirst and the RMS is computed on the result.
Returns:
- xrms : scalar
- as defined above
-
rmsGain(H, f1, f2, N=100)[source]¶ Compute the root mean-square gain of a discrete-time TF.
The computation is carried out over the frequency band
(f1, f2), employingNdiscretization steps.Parameters:
- H : object
- The discrete-time transfer function. See
evalTF()for the supported types. - f1 : scalar
- The start value in Hertz of the frequency band over which the gain is evaluated.
- f2 : scalar
- The end value (inclusive) in Hertz of the aforementioned frequency band.
- N : integer, optional
- The number of discretization points to be taken over specified interval.
Returns:
- Grms : scalar
- The root mean-square gain
-
scaleABCD(ABCD, nlev=2, f=0, xlim=1, ymax=None, umax=None, N_sim=100000.0, N0=10)[source]¶ Scale the loop filter of a general delta-sigma modulator for dynamic range.
The ABCD matrix is scaled so that the state maxima are less than the specified limits (
xlim). As a side effect, the maximum stable input is determined in the process.Parameters:
- ABCD : ndarray
- The state-space description of the loop filter, real or imaginary (quadrature).
- nlev : int, optional
- The number of levels in the quantizer.
- f : scalar
- The normalized frequency of the test sinusoid.
- xlim : scalar or ndarray
- A vector or scalar specifying the limit for each state variable.
- ymax : scalar, optional
- The stability threshold. Inputs that yield quantizer inputs above
ymaxare considered to be beyond the stable range of the modulator. If not provided, it will be set to \(n_{lev} + 5\) - umax : scalar, optional
- The maximum allowable input amplitude.
umaxis calculated if it is not supplied.
Returns:
- ABCDs : ndarray
- The state-space description of the scaled loop filter.
- umax : scalar
- The maximum stable input amplitude. Input sinusoids with amplitudes below this value should not cause the modulator states to exceed their specified limits.
- S : ndarray
- The diagonal scaling matrix.
\(S\) is defined such that:
ABCDs = [[S*A*Sinv, S*B], [C*Sinv, D]] xs = S*x
Where the multiplications are matrix multiplications.
-
simulateDSM(u, arg2, nlev=2, x0=0.0)[source]¶ Simulate a delta-sigma modulator.
Compute the output of a general delta-sigma modulator with input
u, a structure described byABCD, an initial statex0(default zero) and a quantizer with a number of levels specified bynlev.Syntax:
[v, xn, xmax, y] = simulateDSM(u, ABCD, nlev=2, x0=0)[v, xn, xmax, y] = simulateDSM(u, ntf, nlev=2, x0=0)
Parameters:
- u : ndarray or sequence
- The input vector to be used in the simulation. Multiple inputs
are implied by the number of rows in
u. - arg2 : 2D ndarray or a supported LTI description
- The second argument may be either the ABCD matrix describing the
modulator or its NTF. In the latter case, the NTF is converted to
a ZPK description and the structure that is simulated is the
block-diagonal structure used by scipy’s
zpk2ss(). The STF is assumed to be 1. - nlev : int or sequence or ndarray
- Number of levels in the quantizers. Set
nlevto a scalar for a single quantizer modulator. Multiple quantizers are implied by makingnlevan array. - x0 : float or sequence or ndarray
- The initial status of the modulator. If
x0is set to float, its value will be used for all the states. If it is set to a sequence of floats, each of its values will be assigned to a state variable.
Returns:
- v : ndarray
- The quantizer output.
- xn : ndarray
- The modulator states.
- xmax : ndarray
- The maximum value that each state reached during simulation.
- y : ndarray
- The quantizer input (ie the modulator output).
Notes:
Three implementations of this function are (potentially) available to the user, in order of ascending execution speed:
- A CPython implementation, always available.
- A Cython-based implementation requiring the BLAS headers and a compatible compiler.
- A Cython-based implementation accessing the BLAS library pre-compiled through scipy, requiring only a compatible compiler.
The difference in execution time from the first implementation – dynamically interpreted – to the latter two – statically compiled automatically before execution – is a factor 20.
The fastest available implementation is automatically selected.
To assess which implementations are available in your installation, check the
simulation_backendsvariable, for example:from __future__ import print_function import deltasigma as ds print(ds.simulation_backends)
Example output:
{'Scipy_BLAS': True, 'CBLAS': True, 'CPython': True}
Example:
Simulate a 5th-order binary modulator with a half-scale sine-wave input and plot its output in the time and frequency domains.:
import numpy as np from deltasigma import * OSR = 32 H = synthesizeNTF(5, OSR, 1) N = 8192 fB = np.ceil(N/(2*OSR)) f = 85 u = 0.5*np.sin(2*np.pi*f/N*np.arange(N)) v = simulateDSM(u, H)[0]
Graphical display of the results:
(Source code, png, hires.png, pdf)
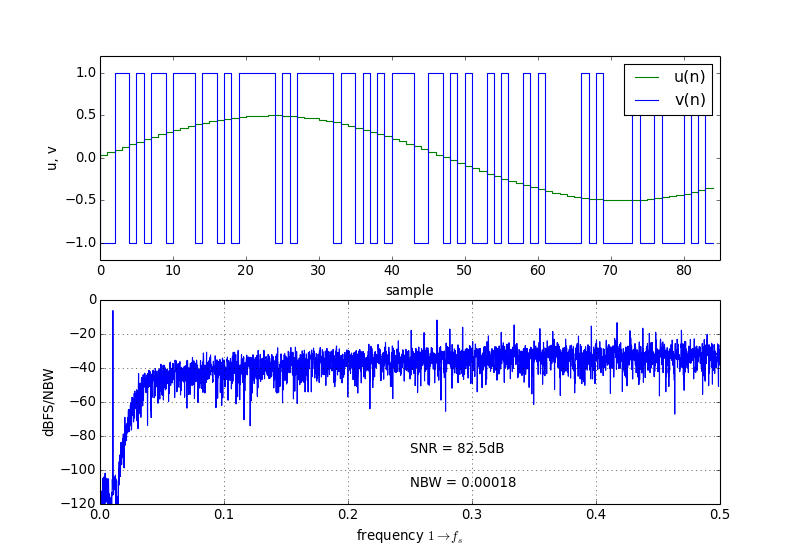
Click on “Source” above to see the source code.
-
simulateQDSM(u, arg2, nlev=2, x0=None)[source]¶ Simulate a quadrature delta-sigma modulator.
This function computes the output of a quadrature delta-sigma modulator corresponding to an input \(u\), with a description of the modulator, an initial state \(x_0\) (default all zeros) and a quantizer whose number of levels is specified by \(n_{lev}\).
For multiple quantizers, make \(n_{lev}\) a 1D vector, for complex quantization to a diamond lattice, multiply \(n_{lev}\) by \(j\).
Regarding the description of the modulator, it may be provided through an ABCD matrix.
In this case, the shapes of the input parameters are:
u.shape = (nu, N),nlev.shape = (nqi,),ABCD.shape = (order+nq, order+nq+nu).
Alternatively, the modulator may be described by a supported TF representation, in particular it is recommended to use a zpk object. In this case, the STF is assumed to be 1.
Parameters:
- u : ndarray
- The input signal to the modulator.
- arg2 : ndarray or a supported LTI representation
- A description of the modulator to simulate.
An ndarray instance is interpreted as an ABCD description. Equivalently,
the ABCD matrix may be supplied in
(A, B, C, D)tuple form. All other supported modulator specifications result in a conversion to a zpk representation. - nlev : int or sequence-like, optional
- The number of levels in the quantizer. If set to a sequence, each of the
elements is assumed to be the number of levels associated with a
quantizer. Defaults to
2. - x0 : float or sequence-like, optional
- The initial states of the modulator. If it is set to a float, all states
are assumed to have the same value,
x0. If it is set to a sequence-like object (list, tuple, 1D ndarray and similar), each entry is assumed to be the value of one of the modulator states, in ascending order. Defaults to0.
Returns:
- v : ndarray
- The quantizer output.
- xn : ndarray
- The modulator states.
- xmax : ndarray
- The maximum value that each state reached during simulation.
- y : ndarray
- The quantizer input (ie the modulator output).
-
simulateQSNR(ntf, R=64, amp=None, f0=0, nlev=2, f=None, k=13)[source]¶ Determine the SNR for a quadrature delta-sigma modulator using simulations.
The modulator is described by a Noise Transfer Function (NTF) and the number of quantizer levels.
Using sine waves located in FFT bins, the SNR is calculated as the ratio of the sine wave power to the power in all in-band bins other than those associated with the input tone. Due to spectral smearing, the input tone is not allowed to lie in bins 0 or 1.
Parameters:
- ntf : tuple, ndarray or LTI object
- The Noise Transfer Function in any form supported by
simulateQDSM(), such as an ABCD matrix or an NTF description, for example a zpk tuple, num-den tuple or an LTI object. If no information is available regarding the STF, it is assumed to be unitary. - R : int, optional
- The oversampling ratio, defining the band of interest. Defaults to 64.
- amp : sequence, optional
- The sequence of the amplitudes to be used for the input signal, in ascending order, expressed in dB, where 0 dB means a full-scale (peak value \(n_{lev}-1\)) sine wave. Defaults to [-120 -110...-20 -15 -10 -9 -8 ... 0] dB.
- f0 : float, optional
- The normalized center frequency of the modulator. Defaults to 0.
- nlev : int, optional
- The number of levels in the modulator quantizer. Defaults to 2.
- f : float, optional
- The input signal frequency, normalized such that \(1 \rightarrow f_s\). It is rounded to an FFT bin. If not set, defaults to \(1/(4\cdot OSR)\).
- k : int, optional
- The integer
ksets the length of the FFT, which is \(2^k\). Defaults to 13.
Returns:
- snr : ndarray
- The calculated SNR.
- amp : ndarray
- The amplitude vector corresponding to the SNR.
-
simulateSNR(arg1, osr, amp=None, f0=0, nlev=2, f=None, k=13, quadrature=False)[source]¶ Determine the SNR for a delta-sigma modulator by using simulations.
Simulate a delta-sigma modulator with sine wave inputs of various amplitudes and calculate the signal-to-noise ratio (SNR) in dB for each input.
Three alternative descriptions of the modulator can be used:
- The modulator is described by a noise transfer function (NTF), provided
as
arg1and the number of quantizer levels (nlev). - Alternatively, the first argument to simulateSNR may be an ABCD matrix.
- Lastly,
arg1may be a function taking the input signal as its sole argument.
The band of interest is defined by the oversampling ratio (
osr) and the center frequency (f0).The input signal is characterized by the
ampvector and thefvariable. A default value forampis used if not supplied.fis the input frequency, normalized such that 1 -> fs;fis rounded to an FFT bin.Using sine waves located in FFT bins, the SNR is calculated as the ratio of the sine wave power to the power in all in-band bins other than those associated with the input tone. Due to spectral smearing, the input tone is not allowed to lie in bins 0 or 1. The length of the FFT is \(2^k\).
If the NTF is complex,
simulateQDSM()(which is slow, also available in a future release) is called.If ABCD is complex,
simulateDSM()is used with the real equivalent of ABCD in order to speed up simulations.Future versions may accommodate STFs.
Parameters:
- arg1 : scipy ‘lti’ object, or ndarray
- The first argument may be one of the various supported representations for an NTF or an ABCD matrix. Quadrature modulators are supported both with quadrature TFs or with quadrature ABCD matrices, the latter being the recommended description.
- osr : int
- The over-sampling ratio.
- amp : sequence, optional
- The amplitudes in dB, referred to the FS, for which the SNR is to be
evaluated.
ampdefaults to [-120 -110...-20 -15 -10 -9 -8 ... 0]dB, where 0 dB means a full-scale (peak value = nlev-1) sine wave. - f0 : float, optional
- The center frequency. Normalized. Defaults to 0.
- nlev : int, optional
- Number of quantizer levels, defaults to 2.
- f : float, optional
- Test signal input frequency. Normalized. Rounded to an FFT bin. Defaults to:
\[f = \frac{1}{4\ \mathrm{OSR}}\]- k : int, optional
- The number of samples used to compute the FFT is set by the integer
k- default value 13 - through the relationship:
\[N_{samples} = 2^k\]- quadrature : boolean, optional
- Whether the delta-sigma modulator is a quadrature modulator or not.
Defaults to
False.
Returns:
- snr : ndarray
- The SNR, from simulation.
- amp : ndarray
- The amplitudes corresponding to the SNR values.
See also
Example:
Compare the SNR vs input amplitude curve for a fifth-order modulator, as computed by the describing function method (
predictSNR()) with that determined by simulation (simulateSNR()).:import pylab as plt from deltasigma import * OSR = 32 H = synthesizeNTF(5, OSR, 1) snr_pred, amp, _, _, _ = predictSNR(H,OSR) snr, amp = simulateSNR(H, OSR) plt.plot(amp, snr_pred, 'b', label='Predicted') plt.hold(True) plt.plot(amp, snr, 'go', label='Simulated') plt.grid(True) figureMagic([-100, 0], 10, None, [0, 100], 10, None) plt.xlabel('Input Level, dB') plt.ylabel('SNR, dB') s = 'peak SNR = %4.1fdB\n' % max(snr) plt.text(-65, 15, s, horizontalalignment='left') plt.legend(loc='best')
(Source code, png, hires.png, pdf)
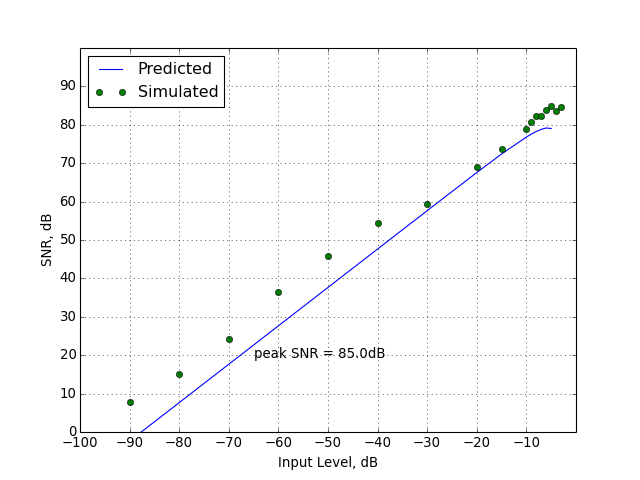
- The modulator is described by a noise transfer function (NTF), provided
as
-
stuffABCD(a, g, b, c, form='CRFB')[source]¶ Calculate the ABCD matrix from the parameters of a modulator topology.
Parameters:
- a : array_like
- Feedback/feedforward coefficients from/to the quantizer. Length \(n\).
- g : array_like
- Resonator coefficients. Length \(floor(n/2)\).
- b : array_like
- Feed-in coefficients from the modulator input to each integrator. Length \(n + 1\).
- c : array_like
- Integrator inter-stage coefficients. Length \(n\).
- form : str, optional
- See
realizeNTF()for a list of supported structures.
Returns:
- ABCD : ndarray
- A state-space description of the modulator loop filter.
See also
mapABCD(), the inverse function.
-
synthesizeChebyshevNTF(order=3, OSR=64, opt=0, H_inf=1.5, f0=0.0)[source]¶ Synthesize a noise transfer function for a delta-sigma modulator.
The NTF is a type-2 highpass Chebyshev function.
synthesizeNTF()assumes that magnitude of the denominator of the NTF is approximately constant in the passband. When the OSR orH_infare low, this assumption breaks down andsynthesizeNTF()yields a non-optimal NTF.synthesizeChebyshevNTF()creates non-optimal NTFs, but fares better thansynthesizeNTF()in the aforementioned circumstances.Parameters:
- order : int, optional
- order of the modulator, defaults to 3
- OSR : int, optional
- oversampling ratio, defaults to 64
- opt : int, optional
- ignored value, for consistency with
synthesizeNTF() - H_inf : float, optional
- maximum NTF gain, defaults to 1.5
- f0 : float, optional
- center frequency (1->fs), defaults to 0.
Returns:
- z, p, k : tuple
- a zpk tuple containing the zeros and poles of the NTF.
Warns:
- If a non-zero value is passed for
opt.
Raises:
- ValueError: Order must be even for a bandpass modulator.
Example:
Compare the NTFs created by
synthesizeNTF()andsynthesizeChebyshevNTF()whenOSRis low:OSR = 4 order = 8 H_inf = 3 H0 = synthesizeNTF(order, OSR, 1, H_inf) H1 = synthesizeChebyshevNTF(order, OSR, 0, H_inf)
(Source code, png, hires.png, pdf)
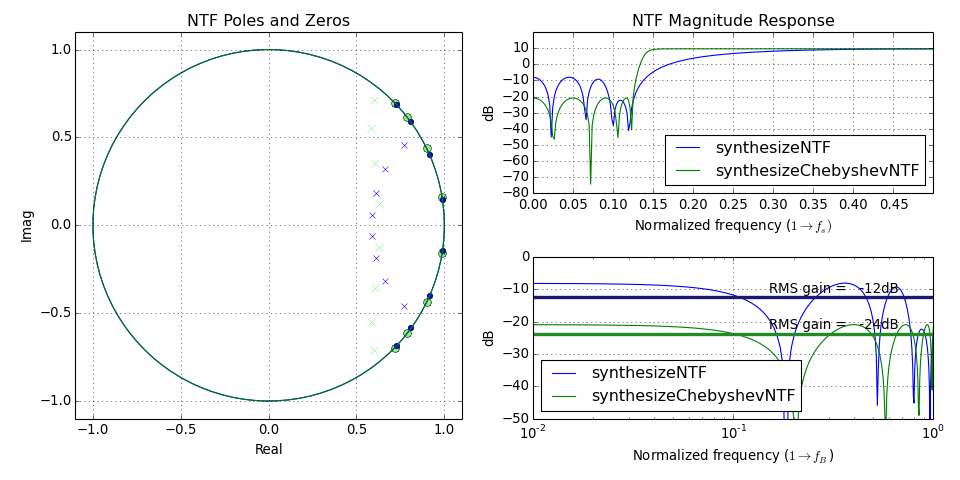
Repeat for
H_inflow:OSR = 32 order = 5 H_inf = 1.2 H0 = synthesizeNTF(order, OSR, 1, H_inf) H1 = synthesizeChebyshevNTF(order, OSR, 0, H_inf)
(Source code, png, hires.png, pdf)
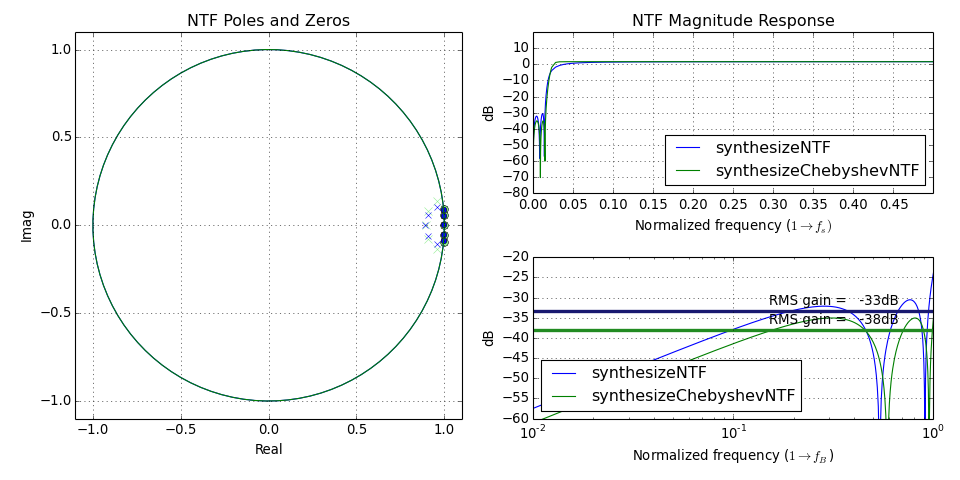
-
synthesizeNTF(order=3, osr=64, opt=0, H_inf=1.5, f0=0.0)[source]¶ Synthesize a noise transfer function for a delta-sigma modulator.
Parameters:
- order : int, optional
- the order of the modulator, defaults to 3.
- osr : float, optional
- the oversampling ratio, defaults to 64.
- opt : int or list of floats, optional
flag to select which algorithm is to be used to place the zeros, defaults to 0.
- 0 -> not optimized,
- 1 -> optimized,
- 2 -> optimized with at least one zero at band-center,
- 3 -> optimized zeros (with optimizer)
- 4 -> same as 3, but with at least one zero at band-center
- [z] -> zero locations in complex form
- H_inf : float, optional
- maximum allowed value of the absolute value of the NTF. Defaults to 1.5.
- f0 : float, optional
- center frequency for band-pass modulators, or 0 for low-pass modulators.
Defaults to 0.
The frequency is normalized throughout the
deltasigmapackage. The normalization is: 1 corresponds to the sampling frequency. Therefore 0.5 is the maximum value that can be assigned tof0.
Returns:
- ntf : tuple
- noise transfer function in zpk form.
Raises:
- ValueError
- ‘Error.
f0must be less than 0.5’, iff0is out of range. - ‘Order must be even for a bandpass modulator.’ if the order is odd and therefore incompatible with the modulator type.
- ‘The
optvector must be of length xxx’ ifoptis used to explicitly pass the NTF zeros and these are in the wrong number.
- ‘Error.
Warns:
- ‘Creating a low-pass NTF.’, if the center frequency is different from zero, but so close to 0 that a low-pass modulator must be designed.
- ‘Unable to achieve specified
H_inf...’, if the desiredH_infcannot be achieved. - ‘Iteration limit exceeded’, if the routine converges too slowly.
Notes:
This is actually a wrapper function which calls the appropriate version of
synthesizeNTF, based on the module control flagoptimize_NTFwhich determines whether to use optimization tools.The parameter
H_infis used to enforce the Lee stability criterion.Example:
Fifth-order low-pass modulator; zeros optimized for an oversampling ratio of 32.:
from deltasigma import * H = synthesizeNTF(5, 32, 1) pretty_lti(H)
Returns:
(z -1) (z^2 -1.997z +1) (z^2 -1.992z +0.9999) -------------------------------------------------------- (z -0.7778) (z^2 -1.796z +0.8549) (z^2 -1.613z +0.665)
(Source code, png, hires.png, pdf)
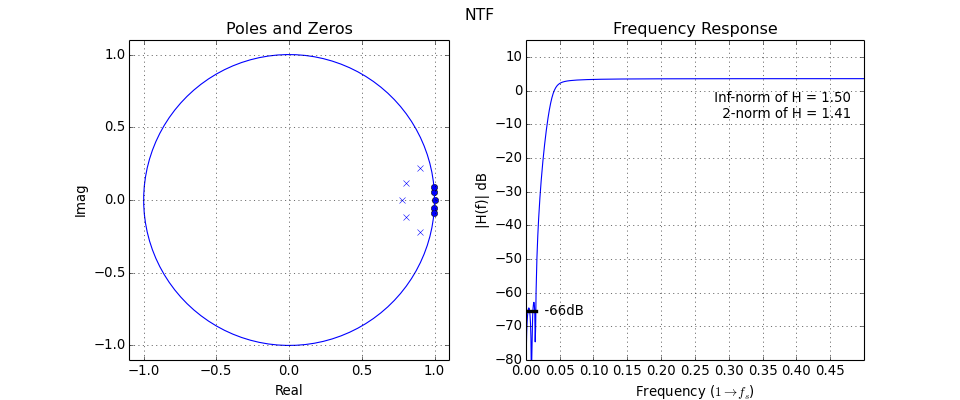
See also
clans(): Closed-Loop Analysis of Noise-Shaper.- An alternative method for selecting NTFs based on the 1-norm of the impulse response of the NTF.
synthesizeChebyshevNTF(): Select a type-2 highpass Chebyshev NTF.- This function does a better job than
synthesizeNTF()ifosrorH_infis low.
-
synthesizeQNTF(order=4, OSR=64, f0=0.0, NG=-60, ING=-20, n_im=None)[source]¶ Synthesize a noise transfer function for a quadrature modulator.
Parameters:
- order : int, optional
- The order of the modulator. Defaults to 4.
- OSR : int, optional
- The oversampling ratio. Defaults to 64.
- f0 : float, optional
- The center frequency, normalized such that \(1 \rightarrow f_s\). Defaults to 0, ie to a low-pass modulator.
- NG : float, optional
- The in-band noise gain, expressed in dB. Defaults to -60.
- ING : float, optional
- The image-band noise gain, in dB. Defaults to -20.
- n_im : int, optional
- The number of in-band image zeros, defaults to
floor(order/3).
Returns:
- ntf : (z, p, k) tuple
ntfis a zpk tuple containing the zeros, poles and the gain of the synthesized NTF.
Note
From the MATLAB Delta-Sigma Toolbox: ALPHA VERSION: This function uses an experimental ad-hoc method that is neither optimal nor robust.
Example:
Fourth order quadrature modulator:
from deltasigma import * order = 4 osr = 32 NG = -50 ING = -10 f0 = 1 / 16 ntf0 = synthesizeQNTF(order, osr, f0, NG, ING) pretty_lti(ntf0)
Returns:
(z - 0.888 - 0.4598j) (z - 0.9239 + 0.3827j) (z - 0.9239 - 0.3827j) (z - 0.953 - 0.3028j) --------------------------------------------------------------------------------------------- (z - 0.5739 - 0.5699j) (z - 0.5913 - 0.2449j) (z - 0.6731 + 0.2788j) (z - 0.8088 - 0.0028j)
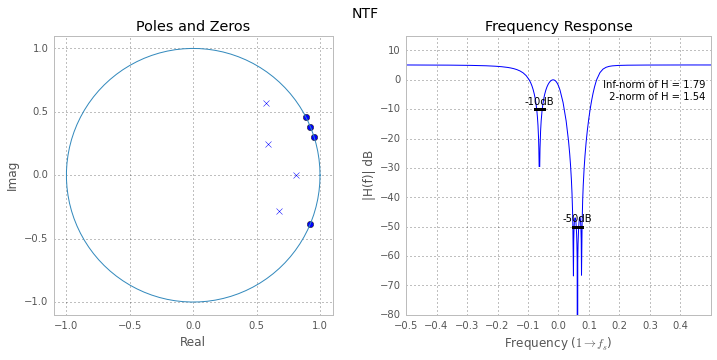
-
undbm(p, z=50)[source]¶ Calculate the RMS voltage equivalent of a power
pexpressed in dBm.\[V_{\mathrm{RMS}} = \sqrt{z\ 10^{p/10 - 3}}\]Parameters:
- p : scalar or sequence
- The power to be converted.
- z : scalar, optional
- The normalization resistance value, defaults to 50 ohm.
Returns:
- Vrms : scalar or sequence
- The RMS voltage corresponding to
p.
-
undbp(x)[source]¶ Convert
xfrom dB to power.The conversion is carried out according to the relationship:
\[P_{\mathrm{RMS}} = 10^{x/10}\]Parameters:
- x : scalar or sequence
- The signal in dB to be converted.
Returns:
- Prms : scalar or sequence
- The RMS power corresponding to
x.
-
undbv(x)[source]¶ Convert
xfrom dB to voltage.The conversion is carried out according to the relationship:
\[V_{\mathrm{RMS}} = 10^{x/20}\]Parameters:
- x : scalar or sequence
- The signal in dB to be converted.
Returns:
- Vrms : scalar or sequence
- The RMS voltage corresponding to
x.
-
cplxpair(x, tol=100)[source]¶ Sort complex numbers into complex conjugate pairs.
This function replaces MATLAB’s cplxpair for vectors.
-
mfloor(x)[source]¶ Round
xtowards -Inf.This is a MATLAB-compatible floor function, numpy’s
floor()behaves differently.If the elements of
xare complex, real and imaginary parts are rounded separately.
-
mround(x)[source]¶ Round
xto the nearest integers.This is a MATLAB-compatible round function, numpy’s
round()behaves differently.Behaviour with a fractional part of 0.5:
- Positive elements with a fractional part of 0.5 round up to the nearest positive integer.
- Negative elements with a fractional part of -0.5 round down to the nearest negative integer.
If the elements of
xare complex, real and imaginary parts are rounded separately.Example:
>>> mround([-1.9, -0.5, -0.2, 3.4, 4.5, 5.6, 7.0, 2.4+3.6j]) [-2.0, -1.0, 0.0, 3.0, 5.0, 6.0, 7.0, 2.0+4.0j]
-
rat(x, tol)[source]¶ Rational fraction approximation.
Calculate A and B such that:
\[x = \frac{A}{B} + \epsilon\]where:
\[\begin{split}|\epsilon| < tol\end{split}\]Note
A, B are of type ‘int’
-
gcd(a, b)[source]¶ Calculate the Greatest Common Divisor of a and b.
Unless b==0, the result will have the same sign as b (so that when b is divided by it, the result comes out positive).
-
lcm(a, b)¶ Calculate the Least Common Multiple of
aandb.
-
zinc(f, m=64, n=1)[source]¶ Calculate the magnitude response of a cascade of
nm-th order comb filters.The magnitude of the filter response is calculated mathematically as:
\[\left|H(f)\right| = \left|\frac{\mathrm{sinc}(m f)}{\mathrm{sinc}(f)}\right|^n\]Parameters:
- f : ndarray
- The frequencies at which the magnitude response is evaluated.
- m : int, optional
- The order of the comb filters.
- n : int, optional
- The number of comb filters in the cascade.
Returns:
- HM : ndarray
- The magnitude of the frequency response of the cascade filter.